operations with Whole Numbers
1. ADDITION AND SUBTRACTION
When we have two whole numbers:
- if both have the same sign, we add their absolute values and put the common sign:
3 + 4 = 7 - 3 - 4 = - 7
- If both have different signs, we subtract the bigger absolute value minus the lower absolute value and put the sign of the number which has bigger absolute value:
3 – 7 = - 4 11 – 7 = 4
When we have more whole numbers:
NOTE: If there is a negative sign before a bracket, we change the sign of the result of the bracket (or the sign of all the numbers inside the bracket) but we don´t change it if the sign before the bracket is positive:
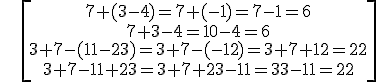
2. MULTIPLICATION AND DIVISION
When we have two whole numbers, we multiply (or divide) their absolute values and:
When we have more than two whole numbers, we use the associative property and we multiply (or divide) in pairs:
-3·(-5)·(-11)= 15·(-11) = -165
-120:(-5):12 = 24:12 = 2
NOTE: Remember the hierarchy of the operations:
A power of a positive whole number is always a positive number:
35 = 243
A power of a negative whole number is either a positive number if the index is an even number, or a negative number if the index is an odd number:
(-3)3 = -27 (-3)4 = 81
Properties of powers:
- Power of a product: (a · b)n = an · bn
Example: 25 · 55 = (2 · 5)5 = 105 = 100.000
- Power of a quotient: (a : b)n = an : bn
Example: 124 : 34 = (12 : 3)4 = 44 = 256
an · am = am+n
Example: 32 · 33 = (3 · 3) . (3 · 3 · 3) = 32+3 = 35 = 243
- Division of powers with the same base:
an : am = am-n
Example: 1225 : 1223 = 1225-23 = 122 = 144
- Power of a power:
(am)n = am·n
Example: (23)2 = 23 · 23 = (2 · 2 · 2)·(2 · 2 · 2) = 23·2 = 26 = 64
- NOTE: a0 = 1 a1 = a
Exercises:
1.- Calculate:
a) -5 + (7-3) - 8·3 + 2:2 =
b) 5 - 3·[3 + 2·2 - 5] + 15 - 12:(6-8) =
c) (-2)4 =
d) (-1)1110003238 =
2.- Reduce to one power:
a) [(-2)4]3:[(-2)3]3=
b) (x7⋅x6):x11=
c) (-12)5:(-3)5=
Solutions: 1.- a) -24; b) 20; c) 16; d) 1; 2.- a) (-2)3; b) x2; c) 45
Obra colocada bajo licencia Creative Commons Attribution Non-commercial Share Alike 3.0 License