Monomials

A monomial is the simplest algebraic expression; it is formed by the product of numbers and letters or variables (with powers) .

It has two parts: the number part is called coefficient, and the letters part is called literal part.

Examples:

·  -4x (-4 is the coefficient and x is the literal part)

·  3xy²z⁵ (3 is the coefficient and xy²z⁵ is the literal part)

·  4x/y isn’t a monomial

The degree of a variable is the index of its power and the degree of the monomial is the addition of the degrees of its variables.

Examples: 4x has degree 1 and 3xy²z⁵ has degree 8.

Two monomials are called similar or like monomials if they have the same literal part.

Examples:

 

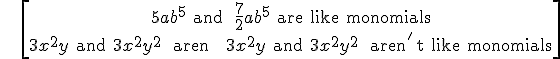
Exercise: Decide if the following expressions are monomials or not, and if they are monomials find their coefficients, literal parts and degrees:

a) -3xy³z⁹

b) πa⁷b⁹c

c) 3x + y

d) 17x/y

e) 4a¹¹b³c²d

 

Solutions: a) coefficient: -3, literal part: xy³z⁹; degree: 13; b) coeff.: π, lit. p.: a⁷b⁹c, deg: 17; c) it isn't monomial; d) it isn't monomial;

               e) coeff.: 4, lit. p.: a¹¹b³c²d , deg: 17