Quadratic equations
You can always reduce a quadratic equation to this form, which is called general form:
![]()
Examples:
1) 3x2 - 5x + 2 = 0 a = 3 b = -5 c = 2
2) x2 – 3 = 0 a = 1 b = 0 c = -3
3) 2x2 – 100x = 0 a = 2 b = -100 c = 0
4) (x + 2) · (x – 3) = 14; x2 + 2x – 3x – 6 = 14
x2 + 2x – 3x – 6 – 14 = 0
x2 – x – 20 = 0; a = 1, b = -1, c = -20
The solutions to this one are x = 5 and x = -4
To solve a quadratic equation, we have to use the formula:

Example 1:
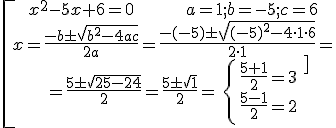
Example 2:
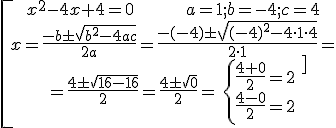
Example 3:
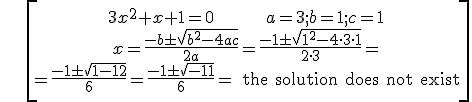
Example 4:
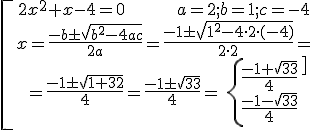
NOTE: The discriminant, Δ = b2 – 4ac, is the value which detemines the number of solutions: if Δ > 0 there are two solutions; if Δ = 0 there is one solution and if Δ < 0 there is no solution.
INCOMPLETE EQUATIONS
Example 5: b = c = 0
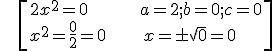
Example 6: b = 0
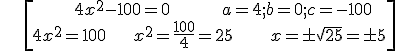
Example 7: c = 0
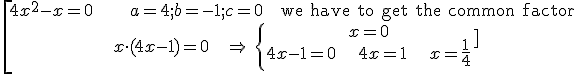
Example 8: c = 0
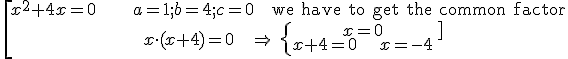
Exercise: solve the following quadratic equations:
a) x2 - 5x + 4 = 0
b) x2 - 18x + 81 = 0
c) x2 + x + 15 = 0
d) x2 - 7x = 0
e) 147x2 = 0
f) 4x2 - 9 = 0
Solutions: a) 1 and 4; b) 9; c) Φ; d) 0 and 7; e) 0; f) ±3/2
Licensed under the Creative Commons Attribution Non-commercial Share Alike 3.0 License