Sequences and progressions
Sequences
A sequence is an ordered set of numbers (or other objects), arranged according to a rule.
For example:
· 1, 2, 3, 4, 5, …
· 2, 4, 6, 8, 10, …
· 1, 4, 9, 16, 25, …
· 32, 16, 8, 4, 2, …
· 1, 1, 2, 3, 5, 8, 13, …
Each number of the sequence is called term, and we represent it as ai. We call general term of a sequence, an, the expression which represents any term of the sequence.
For example:
· 1, 2, 3, 4, 5, … an = n, then a100 = 100
· 2, 4, 6, 8, 10, … an = 2n, then a25 = 50
· 1, 4, 9, 16, 25, … an = n2, then a12 = 144
· 32, 16, 8, 4, 2, … an = 26-n, then a10 = 2-4 = 1/16
Some sequences are recurring, because we obtain each term from the previous one. For example:
1, 1, 2, 3, 5, 8, 13, … an = an-1 + an-2 a1 = a2 = 1
This is the Fibonacci sequence.
Exercises:
1.- Find out the general term of these sequences:
a) 3, 6, 9, 12, 15, .....
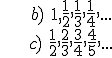
2.- Write the first five terms of the sequences whose general terms are:
a) an = n2 + 1
b) an = 3 - n
![]()
Solutions: 1.- a) an = 3n; b) an = 1/n; c) an = n/(n+1)
2.- a) 2, 5, 10, 17, 26,... b) 2, 1, 0, -1, -2,... c) 2, 3/4, 4/9, 5/16, 6/25,...
Licensed under the Creative Commons Attribution Non-commercial Share Alike 3.0 License