equations of degree greater than 2

If P(x) is a polynomial, then:

x = r is a root of P(x) ↔ (x- r) is a factor of P(x)

x = r is a root of P(x) ↔ x = r is a solution of P(x) = 0

That’s why the solutions of the equation are also called “roots of the equation”.

Then, to solve an equation of degree bigger than two, we have to decompose the polynomial.

Example:

if we apply the Ruffini´s rule two times with -1 and -2, we get in the quotient 4x² - 8x + 3

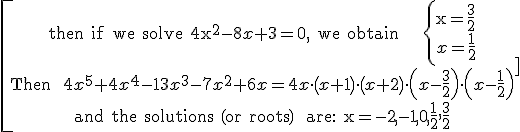
Exercise. Solve the following equations:

a) x⁵ - x⁴ - 5x³ - 3x² = 0

b) 2x⁴ - 11x³ + 18x² - 4x - 8 = 0

Solutions: a) -1, 0, 3; b) -1/2, 2