Trigonometric ratios

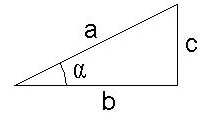
If we have a right-angled triangle, and one of its acute angles is a, then we define its sine, cosine and tangent as:

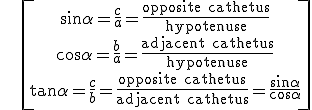
And their inverse ratios, cosecant, secant and cotangent:

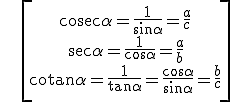
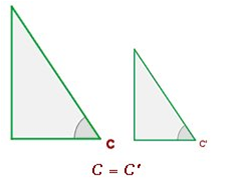
If you apply Thales’ Theorem, you can check that the ratios don’t depend on the lengths of the sides:

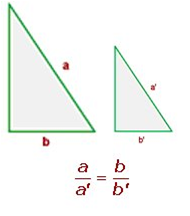Example 1: 45^o  

 

 

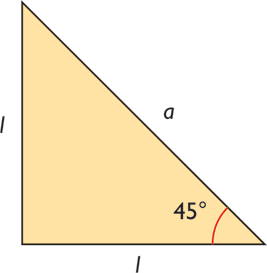
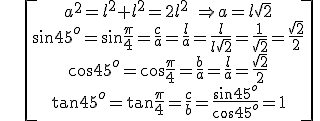
Example 2: 30^o and 60^o

 

 

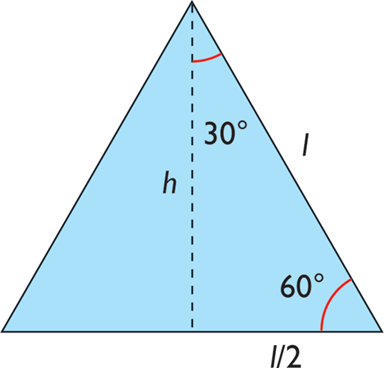
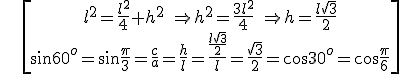
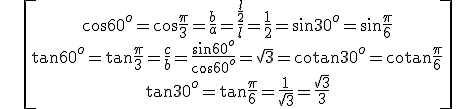
Exercises:

1.-  Calculate the following trigonometric ratios:

a) sin 15^o 45' 40''

b) tan 191^o 15' 12''

2.-  Calculate the angles knowing that:

a) sin α = 0,37

b) cos β = 0,8

3.- In a right-angled triangle, the catheti measure 3 and 4 and the hypotenuse measures 5. Calculate the ratios of its acute angles.

 

 

Solutions:

1.- a) 0,27; b) 0,198

2.- a) 21^o 42' 56''; b) 38^o 39' 35''

3.- sinα = cosβ = 3/5; cosα = sinβ = 4/5; tanα = cotanβ = 3/4