DEFINITE INTEGRAL
We are going to calculate the area under the graph of a function in an interval, the area of R.
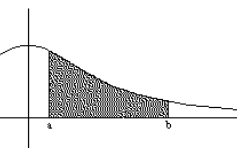
To get it, we do a partition, Pn, of the interval [a,b] in n subintervals:
a = x0<x1<x2<……<xn = b
Then, we have two options to calculate the area:
•The lower sum of f associates to the partition Pn, (lower area) sPn(f)
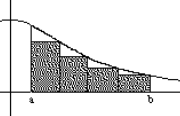
•The higher sum of f associates to the partition Pn, (higher area) SPn(f)

Obviously: sPn(f)≤ area (R) ≤ SPn(f)
If we choose another partition, Pn’, n’ > n, then:


sPn(f)≤ sPn’(f)≤ area (R) ≤ SPn’(f) ≤ SPn(f)
If we do the limits as n approaches ∞ and they are equal, then:
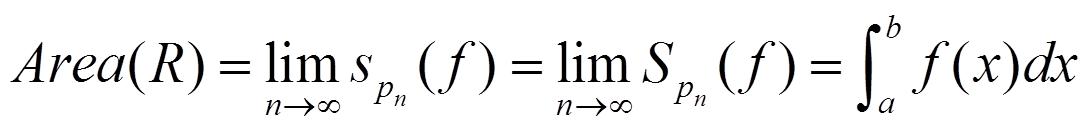
this is called definite integral of f between a and b, and it is said that f is integrable in [a,b]