Invertible matrix
A matrix
![]()
is invertible if
![]()
so that A·B = B·A = In . Otherwise it is called singular matrix.
B=A-1 is called the inverse of A
NOTE:
![]()
![]()
Properties:
Let
![]()
invertibles, then:
![]()
![]()
![]()
Calculation of the inverse by Gauss-Jordan method
To calculate the inverse of an invertible matrix A, we have to transform the matrix (A|I) into the matrix (I|A-1) by using these elementary operations:
- To exchange two rows: Ri ↔ Rj
- To substitute a row by a linear combination of all the rows: Ri↔ k1R1+k2R2+…+kiRi+…kmRm ki ≠ 0, kj are real numbers, j = 1, 2, ….m
Example:
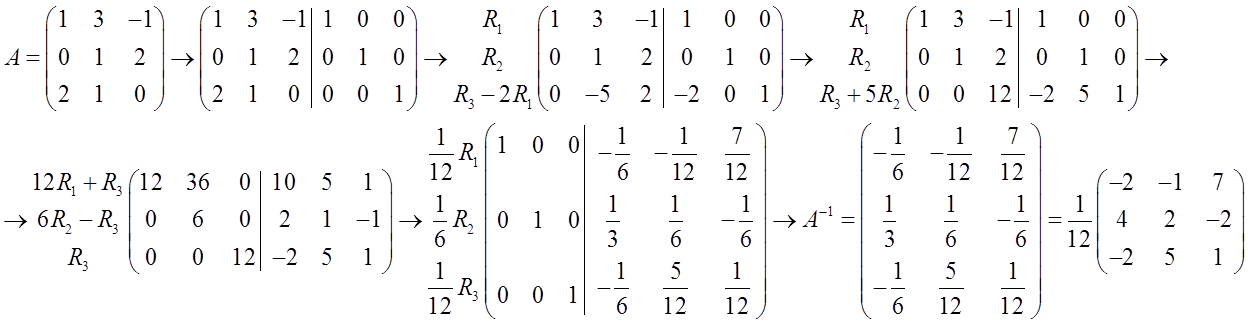
NOTE: if we obtain a row of zeros in the matrix on the left, A is a singular matrix
Exercise. Calculate the inverse of the following matrices:
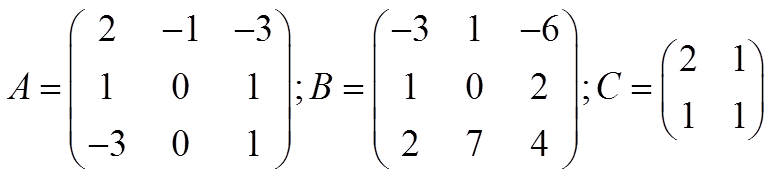
Solutions:
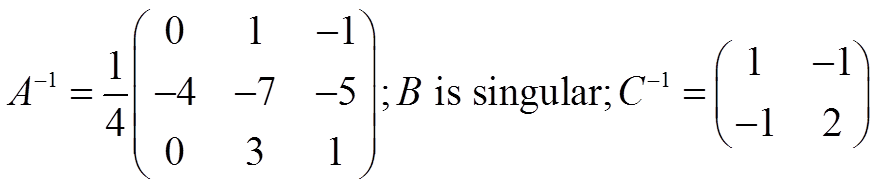
Licensed under the Creative Commons Attribution Non-commercial No Derivatives 3.0 License