Law of total probability

Let A₁, A₂,…,A_n events. They form a complete system of events if:

–A₁UA₂U…UA_n = E

–they are independent in pairs (A_i∩A_j = ф, i,j = 1, 2,…,n)

Law of total probability: Let A₁, A₂,…,A_n a complete system of events with P(A_i) ≠ 0, i = 1, 2,…,n. Let B another event which we know P(B/A_i), i = 1, 2,…,n. Then:

 

Example: A transport company has three routes within a county. 60% of its buses cover the first route, 30% the second and 10% the third. It is known that the daily probabilities of a breakdown in each route are 2%, 4% and 1%, respectively. Find out the probability for a bus to have a breakdown anyday.

 

 

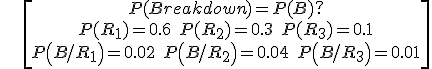
Exercise: (PAEG- June 2013) A company produces two types of parts: A and B. 20% of parts are type A and 80% are type B. The probability that type A part is defective is 0.02 and the probability that a type B part is defective is 0.1. If we choose a part randomly, what is the probability that it is defective?

 

 

 

 

 

 

 

Solution: 0.084