Bolzano's Theorem

If f is continuous in [a,b] and f(a)·f(b) < 0, then

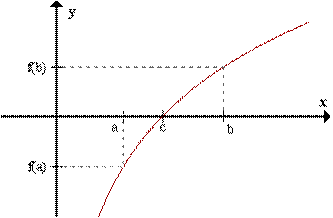
NOTE: this theorem is a tool to approximate a root of an unsolvable equation or to show that it exists.

 

Example: demonstrate that the equation  x³ – 3x + 40 = 0 has a real root and approximate it to the tenths.

  Let f(x) = x³ – 3x + 40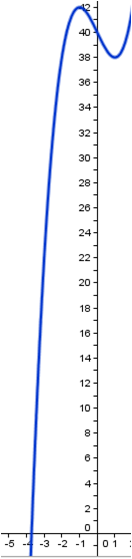   

  f is continuous in R, because it is a polynomial function, and f(-4) = -12, f(-3) = 22, then, using the Bolzano’s Theorem, c exists in (-4,-3) such that f(c) = 0

  ↔ c³ – 3c + 40 = 0↔ c is a root of the equation.

  In addition f(-3,8) = -3,472 and f(-3,7) = 0,447 then, using again the Theorem, c ≈-3,7

 

Exercises

1.- (PAEG- june 2009): Demonstrate that the graphs of the functions:

intersect at least in one point.

2.- The function

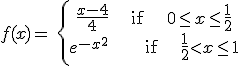
is defined in the interval [0,1] and f(0)·f(1)<0, but doesn't exist any c in [0,1] such that f(c) = 0. Does it contradict Bolzano's Theorem?

 

 

 

Solutions: 1.- Use Bolzano's Theorem for the function f - g; 2.- It doesn't contradict Bolzano's Theorem because f is not continuous in [0,1]