Equations
There are two sides in an equation with an algebraic expression in each one.
Each monomial is a term of the equation.
“x” is called the variable or the unknown.
The degree of an equation is the biggest degree of its terms. If the degree is 1, we call it a linear equation and if the degree is 2 we call it a quadratic equation.
Examples:
· x2 – 3x + 1 = 5x -17 is a quadratic equation
· x + 5 – 3(x + 2) = 5x is a linear equation
Two equations are equivalent if they have exactly the same solutions.
3x = 6 is equivalent to x = 2
To solve an equation is to find the simplest equivalent equation that gives us the solution.
To obtain an equivalent equation we can do only two basic operations:
- Add or subtract the same expression in both sides of the equation.
- Multiply or divide by the same number (except zero) in both sides of the equality.
Exercise: Find the error

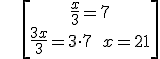
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0