operations with monomials

A. ADDITION AND SUBTRACTION

We can only add or subtract like monomials. Then we add or subtract the coefficients of the monomials and put the same literal part.

Examples:

  3x + 4x = 7x

  5abc² – 4abc² = abc²

  x + x² = x + x²

 

B. MULTIPLICATION

To multiply monomials, we multiply the coefficients and the literal parts separately (remember how we multiply powers with the same base):

      3x · 5x = 3 · 5 · x · x = 15x²        

      -3b · 2b² = -6b³

To multiply a monomial by an addition, we use the distributive property:

    3·(x + 2) = 3·x + 3·2 = 3x + 6

    2x·(x + 1) = 2x·x + 2x·1 = 2x² + 2x

 

C. DIVISION

To divide monomials, we divide the coefficients and the literal parts if we can (remember how we divide powers with the same base), so we obtain another monomial or an algebraic fraction:

 

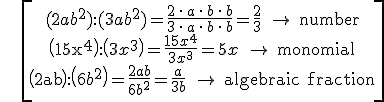
Exercise: calculate:

a) 3x² + 2x³ + 5x² + 23 - 3x³ + 8 =

b) 3ab³ - 3a³b + 5ba³ - 5b³a + 2ab =

c) (-3ab⁵)·(2a²b³c) =

d) (-12x²y²)·(3x³y⁷) =

e) (7a⁵b³c²):(2a²b²c²) =

f) (15x⁴y⁴):(3x²y⁵) =

 

 

 

 

Solutions: a) -x³ + 8x² + 31: b) -2ab³ + 2a³b + 2ab; c) -6a³b⁸c; d) -36x⁵y⁹: e) (7/2)a³b; f) 5x²/y