operations with polynomials
A. ADDITION
To add polynomials, we only have to add their monomials.
Example:
(2x3 + 3x2 – 5x + 2) + (5x2 – 3x + 21) = 2x3 + 3x2 – 5x +2 + 5x2 - 3x + 21 = 2x3 + 8x2 – 8x + 23
B. SUBTRACTION
The opposite of a polynomial is another polynomial with the opposite monomials.
For example:
Op (3x4 – 2x2 + x – 1) = -3x4 +2x2 – x + 1
To subtract polynomials, we only have to add the first polynomial plus the opposite of the second polynomial.
Example:
(2x3 + 3x2 – 5x + 2) - (5x2 – 3x + 21) = 2x3 + 3x2 – 5x +2 - 5x2 + 3x - 21 = 2x3 - 2x2 – 2x - 19
C. MULTIPLICATION
To multiply a polynomial by a monomial, we have to multiply the monomial by each monomial in the polynomial (distributive property).
Example:
(5x3 – 3x2 + 1) · 2x2 = (5x3 · 2x2) – (3x2 · 2x2) + +(1 · 2x2) = 10x5 – 6x4 + 2x2
To multiply two polynomials, we have to multiply each monomial in one polynomial by the other polynomial.
Example:
(5x3 – 3x2 + 1) · (2x2 + 3) = (5x3 · 2x2) – (3x2 · 2x2) + (1 · 2x2) + (5x3 · 3) -(3x2 · 3) + (1 · 3) = 10x5 – 6x4 + 2x2 +15x3 – 9x2 + 3 =
= 10x5 – 6x4 +15x3 – 7x2 +3
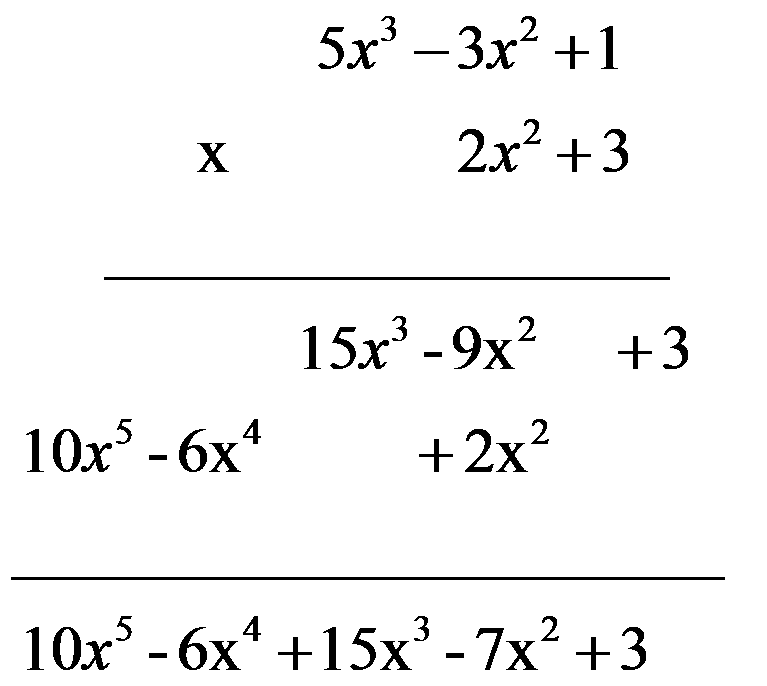
Licensed under the Creative Commons Attribution Non-commercial Share Alike 3.0 License