Factorization of polynomials

A number a is a root of the polynomial P(x), if P(a)=0.

Then, using the remainder Theorem, if we divide P(x) by x – a, the division is exact. Using the division formula: P(x) = Q(x) · (x – a). Therefore we can decompose the polynomial using its roots, remarkable identities, the second degree equation, getting the common factor and the Ruffini’s rule.

Example: decompose x³ -7x + 6

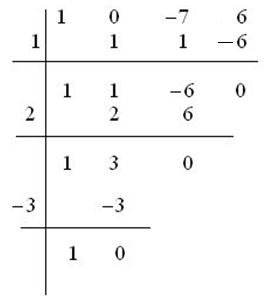
x³ -7x + 6 = (x – 1)·(x – 2)·(x + 3)

NOTE: try only divisors of the numerical term of the polynomial.

Exercise: Factorize the following polynomials:

a) x³ - 9x² + 27x - 27

b) x⁴- x³ - 21x² + 45x

c) 9x³ - 9x² - x + 1

Solutions: a) (x - 3)³ ; b) x·(x - 3)² ·(x +5) ; c) 9·(x - 1)·(x + 1/3)·(x - 1/3)