Ruffini's rule

Ruffini’s rule is a method that simplifies the operations in a division whose divisor is x – a.

To do it, we put the coefficients of the dividend in a row and multiply the first coefficient by a and we add it to the next, and so on.

Examples:

1) if we divide x³ -3x² + x + 2 by x – 3:

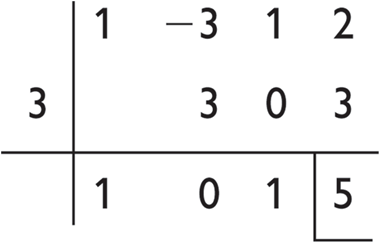     quotient is x² + 1 and the remainder is 5

2) if we divide x⁴ – 16 by x + 2:

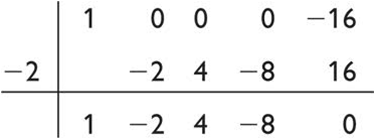   quotient is x³ – 2x² +4x – 8 and the remainder is 0

Exercise: divide:

a) (x³ - 5x² + 3x + 1):(x - 3)

b) (x⁴ - 2x² + x - 1):(x + 1)

Solutions: a) quotient = x² - 2x - 3, remainder = -8; b) quotient = x³ - x² -x + 2, remainder = -3