Other characteristics

A function is called increasing in an interval if, for all x1 and x2 in the interval such that x1 < x2, then f(x1) < f(x2).

A function is called decreasing in an interval if, for all x1 and x2 in the interval such that x1 < x2, then f(x1) > f(x2).

The maximum and minimum of a function, known collectively as extrema, are the largest and smallest value that the function takes at a point either within a given neighbourhood (local or relative extremum) or on the function domain in its entirety (global or absolute extremum).

Examples:
 
 
 
 
 
Exercise: find the extrema, increasing and decreasing intervals of these functions:
 
a)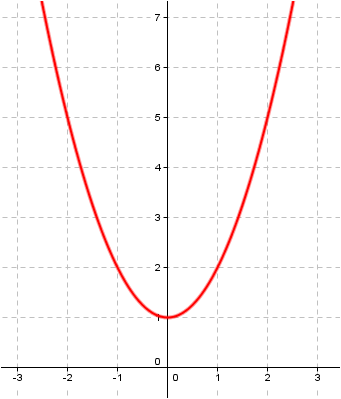 
b)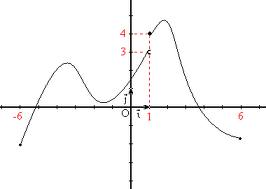
 
 
 
 
 
 
 
Solutions:
function increasing decreasing rel max rel min abs max abs min
a) (0,∞) (-∞,0) Φ 0 Φ 0
b) (-∞,-3.5)U(-1.5,1)U(1,2) (-3.5,-1.5)U(2,∞) -3.5,2 -1,5 2 Φ

Licensed under the Creative Commons Attribution Non-commercial Share Alike 3.0 License