Affine functions

A function is affine if it has this algebraic expression: y = f(x) = mx + n (m,n  € R), with a polynomial of degree 0 or 1.

Its graph is a straight line, where m is called slope and n is called y-intercept.

- If m > 0 the function is increasing

- If m < 0 the function is decreasing

Example: f(x) = 3x + 2
                               3 is the slope and 2 the y-intercept

 

If we have either 2 points or a point and the slope of an affine function, we can find the algebraic expression.

 

With two points, we calculate m as the average rate of change in this interval and then we get n by substituing a point in the formula.

 

With one point and the slope, we get the n as before.

 

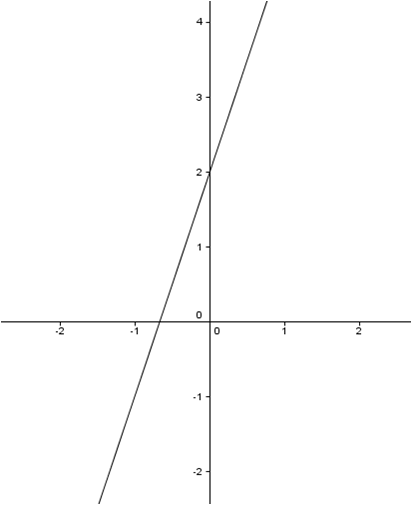
Example: if we have the points (1,1) and (3,4):

 

 

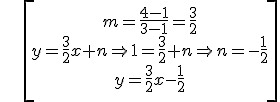
Exercise: find out these affine functions, knowing that:

a) m=3 and its graph passes through the point (1,-5)

b) Its graph passes through the points (0,3) and (1,1)

 

 

 

 

 

 

Solutions: a) y = 3x - 8;  b) y = -2x + 3