Continuity and derivability
THEOREM: If a function f is derivable in x = a, then f is continuous in x = a, too.
demonstration: we have to check that
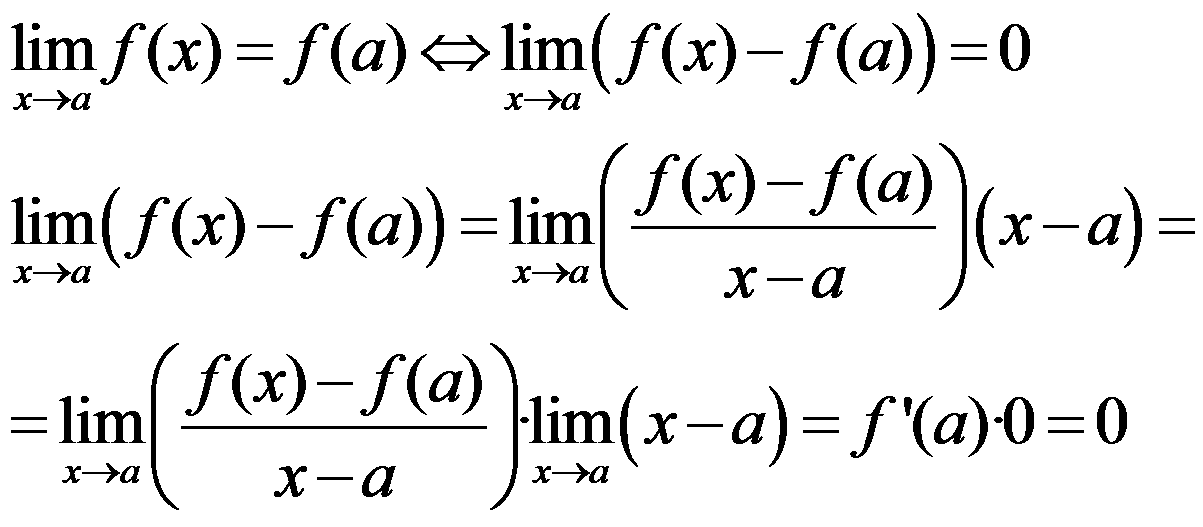
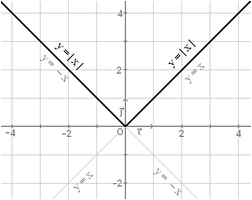
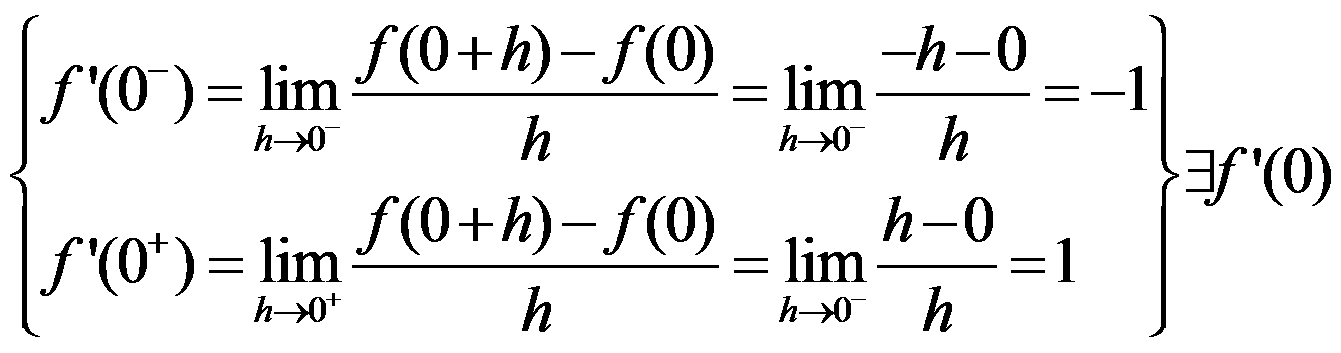
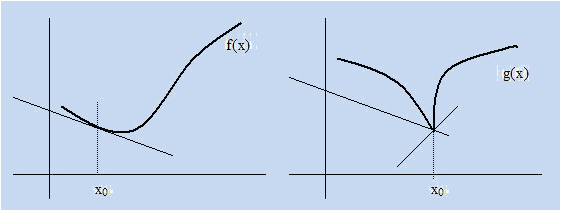
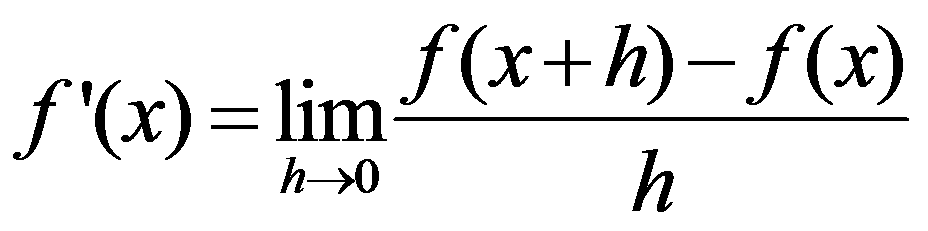
•We only have to study the derivability of a function at the points which the function is continuous. At these points we have to check if the lateral limits (one-sided or lateral derivatives) are equal, f’(a-) = f’(a+) (left derivative = right derivative).
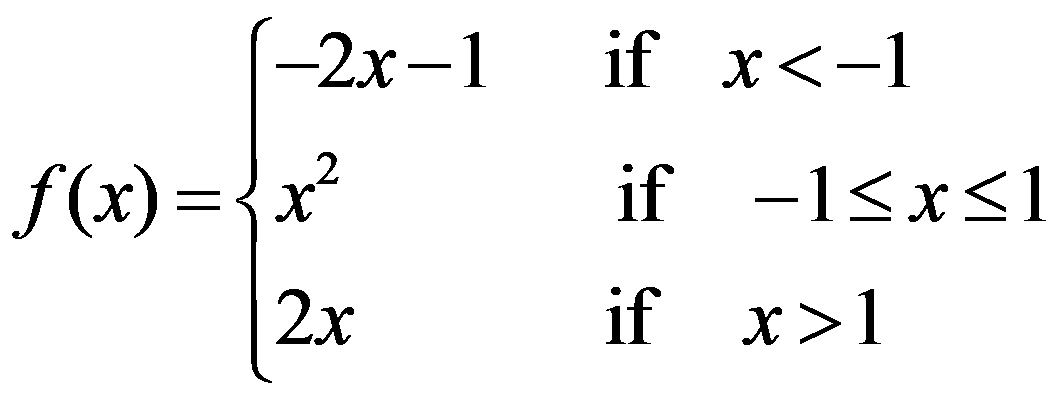
f is derivable in R-{1}
Exercises:
1.- Find the derivative function of:
![]()
2.- Find the abscissa in which the slope of the tangent line to the graph of f(x) = x2 + 1 is 6.
3.- Study the derivability of
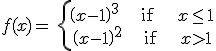
4.- Find the value of a and b to do the function
![]() continuous and derivable in R
continuous and derivable in R
Solutions: 1. f'(x) = -2/x2; b) f'(x) = 2x; 2. x = 3; 3. f is derivable in R; 4. a = 2, b = -1
Licensed under the Creative Commons Attribution Non-commercial Share Alike 3.0 License