Derivative

The rate of change of a function f in an interval [x₁,x₂] is:

RC = f(x₂) – f(x₁)

The average rate of change of a function f in an interval [x₁,x₂] is

Example: f(x) = x²

- If f is decreasing in the interval, then ARC < 0

- If f is increasing in the interval, then ARC > 0

- If f is constant in the interval, then ARC = 0

Let f defined in an open interval centered at a, the derivative, f’(a), of a function y = f(x) in x = a is the limit:

When the function is continuous and the limit exists, we say that f is derivable in x = a.

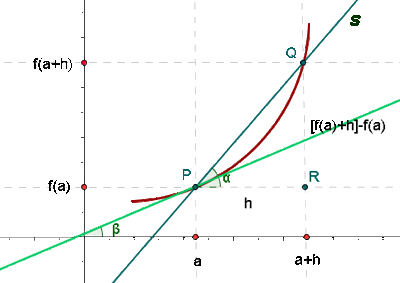
As you can see, the derivative is the slope of the tangent line at the curve in this point. It is also called instantaneous rate of change.

The equation of the tangent line to the curve at the point is:

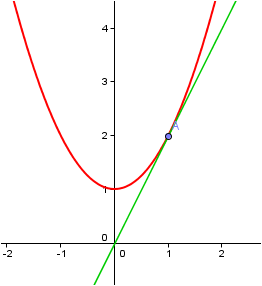
Example: if f(x) = x² + 1, calculate f’(1) and the tangent line at this point.

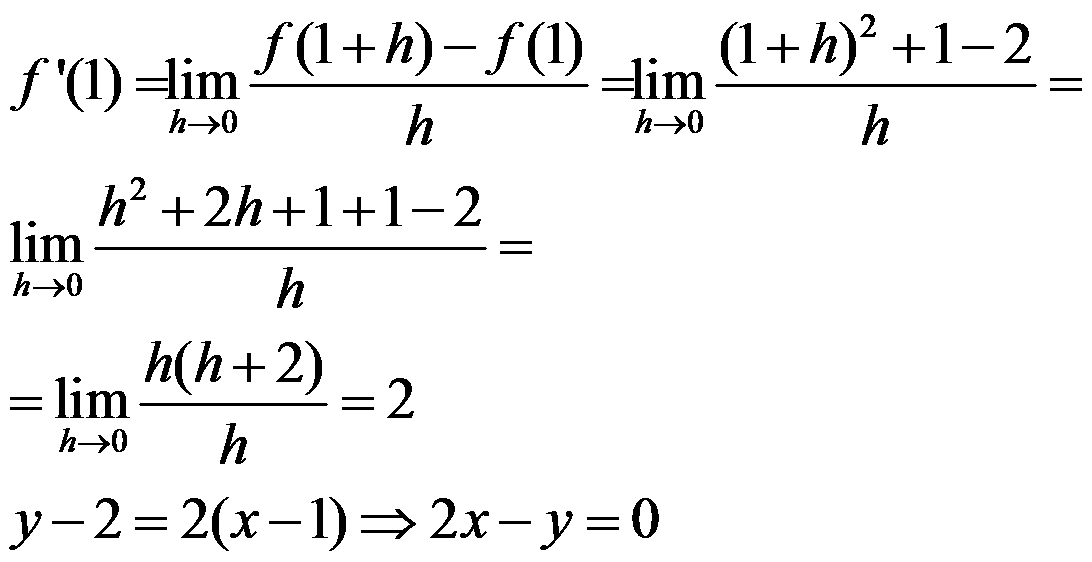
Exercises:

1) Calculate the average rate of change of these functions in the intervals:

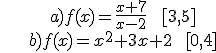
2) Calculate the derivative of these functions at these points by using the definition:

Solutions:1) a) -3; b) 1; 2) a) 1; b) 5