Definite integrals

We are going to calculate the area under the graph of a function in an interval, the area of R

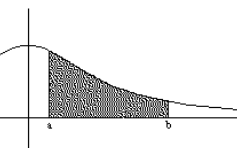
To get it, we do a partition, P_n, of the interval [a,b] in n subintervals:

a = x₀<x₁<x₂<……<x_n = b

Then, we have two options to calculate the area:

- The lower sum of f associates to the partition P_n, (lower area) s_Pn(f)

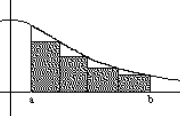
- The higher sum of f associates to the partition P_n, (higher area) S_Pn(f)

Obviously:

s_Pn(f)≤ area (R) ≤ S_Pn(f)

If we choose another partition, P_n’, n’ > n, then:

s_Pn(f)≤ s_Pn’(f)≤ area (R) ≤ S_Pn’(f) ≤ S_Pn(f)

If we do the limits as n approaches ∞ and they are equal, then:

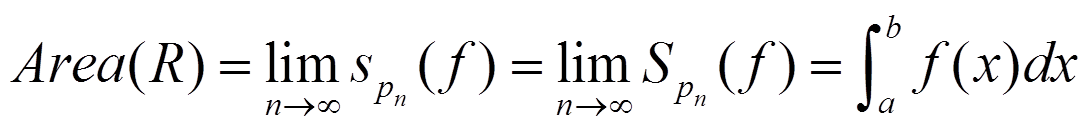
this is called definite integral of f between a and b, and it is said that f is integrable in [a,b]

GeoGebraTube

Definite integral

Approximation to a concept of definite integral

Creado con GeoGebra – Compartida por vmonterreal