SystemsOfEquationsGaussianElimination
Gaussian elimination
The Gaussian elimination is a generalization of the elimination method. The target is, by using the elementary operations, to get the system into a row echelon form:
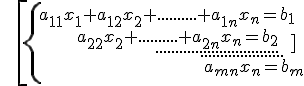
This kind of system lets us find a solution in a simple way.
We can check that every system is equivalent to a system in a row echelon form.
Let r the total of equations and r’ the total of non absurd equations of the system in the row echelon form, then:
–If r ≠ r’ it is an inconsistent system
–If r = r’ it is a consistent system
· If r = r’ = n it is an independent system
· If r = r’ ≠ n it is a dependent system
Where n is the number of unknowns.
NOTE: try to reorder the systems to do a11= ±1
Examples:
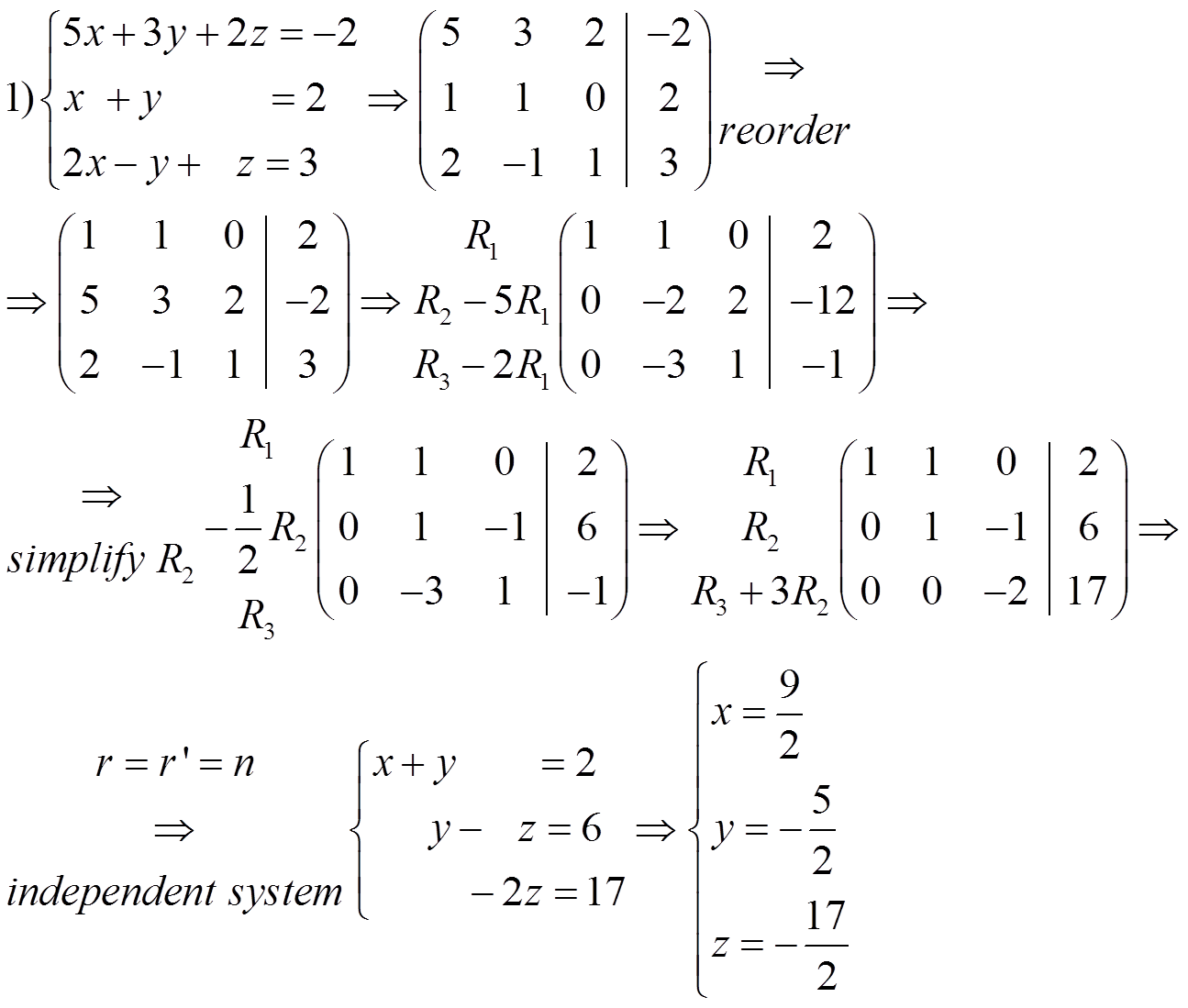
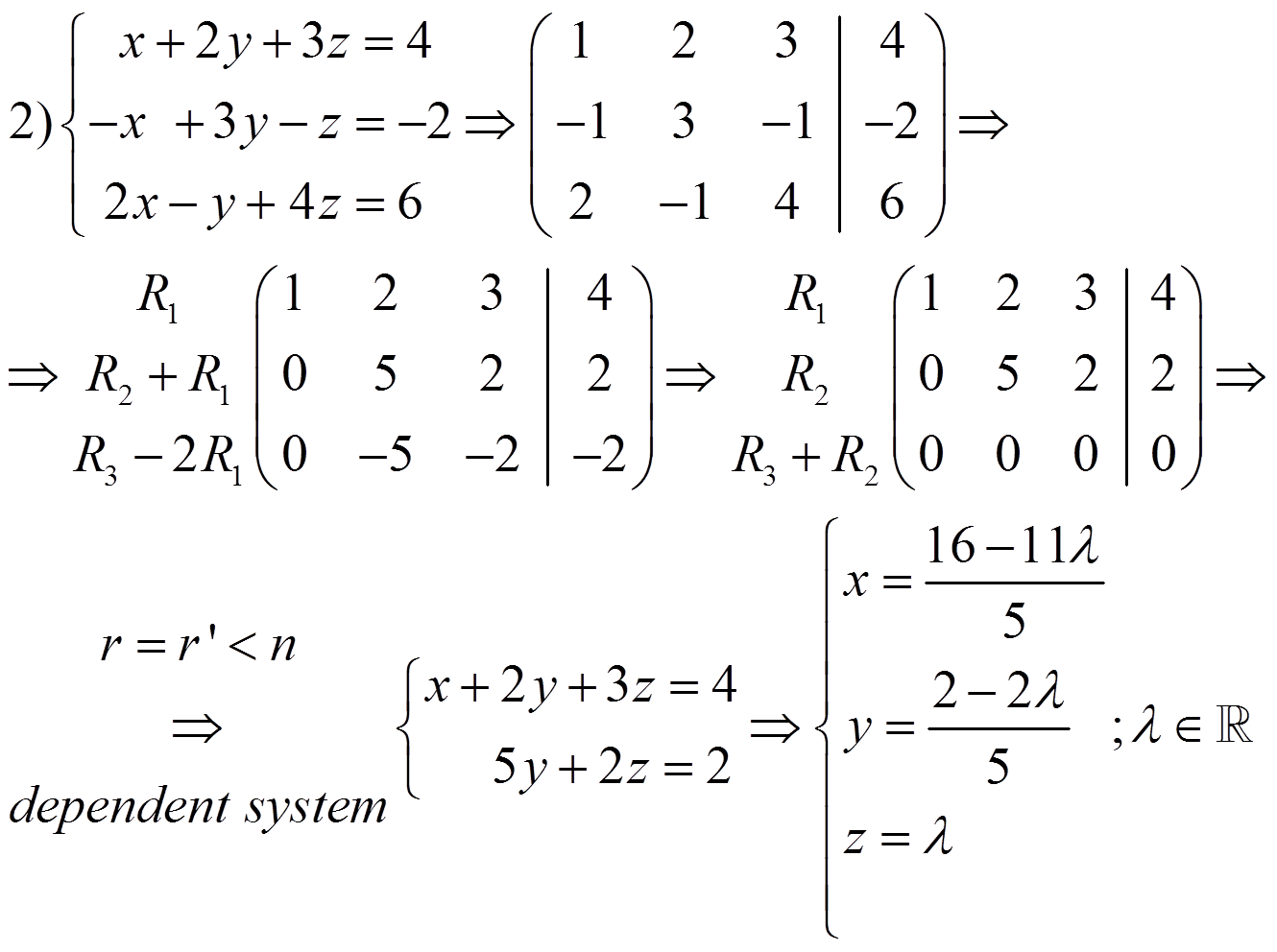
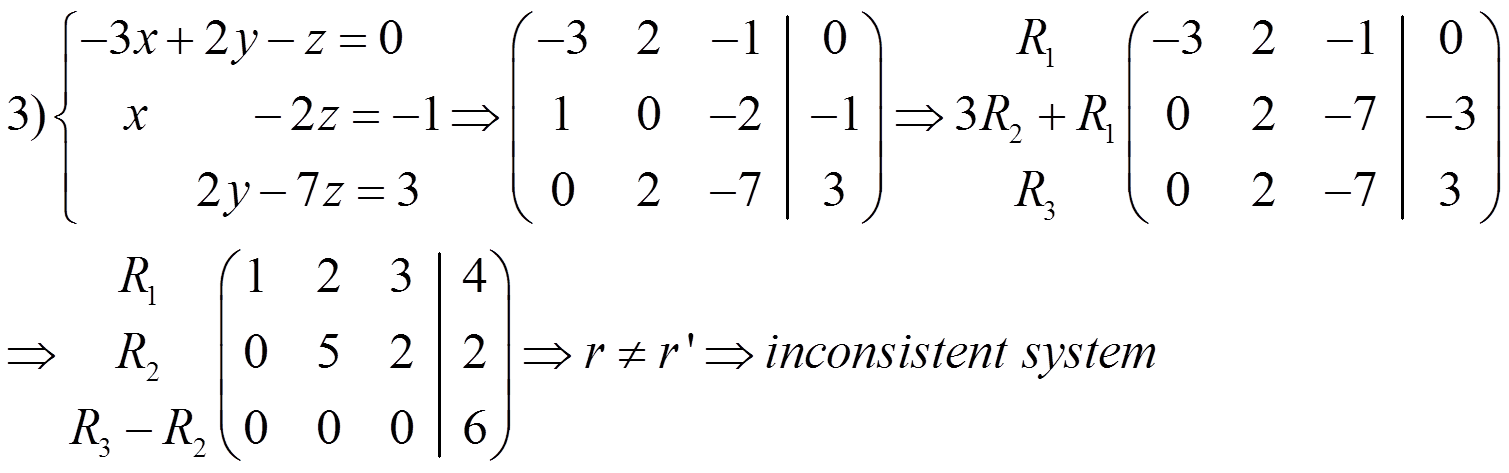
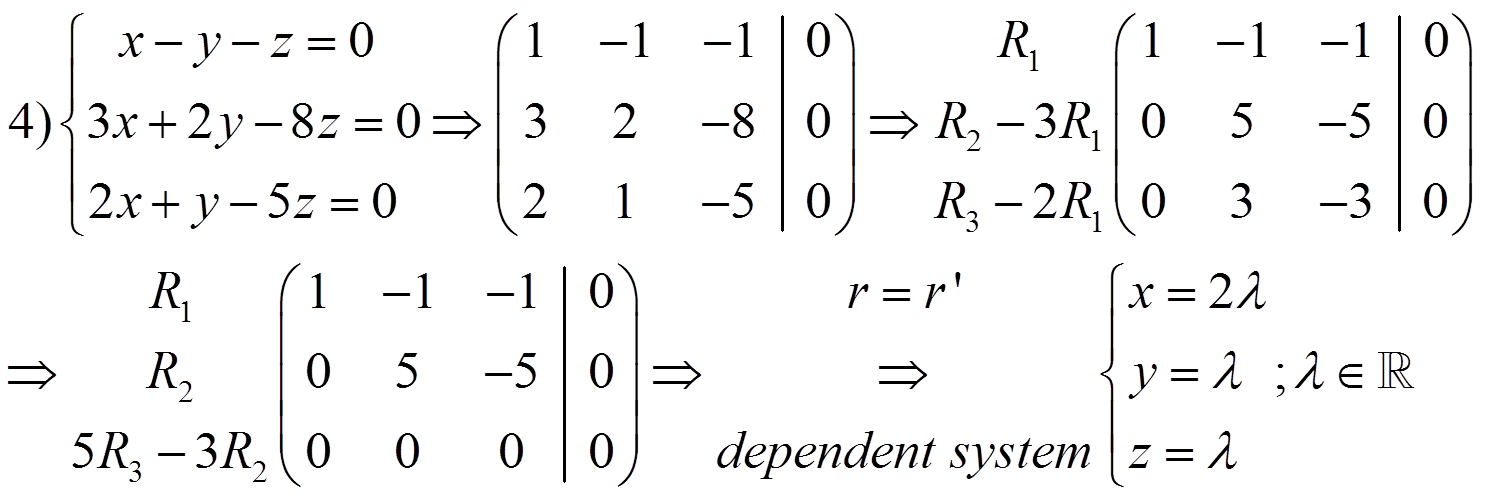
To discuss a system is to determine if it is a consistent or inconsistent system. If it has some parameters, we have to discuss the system depending on the parameters.
Examples:
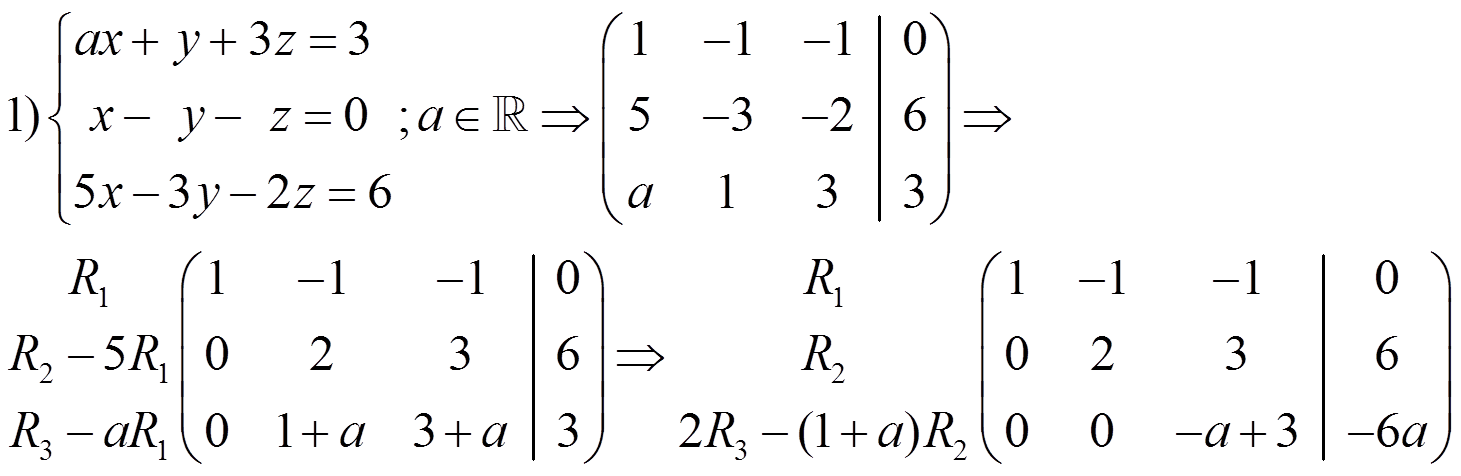
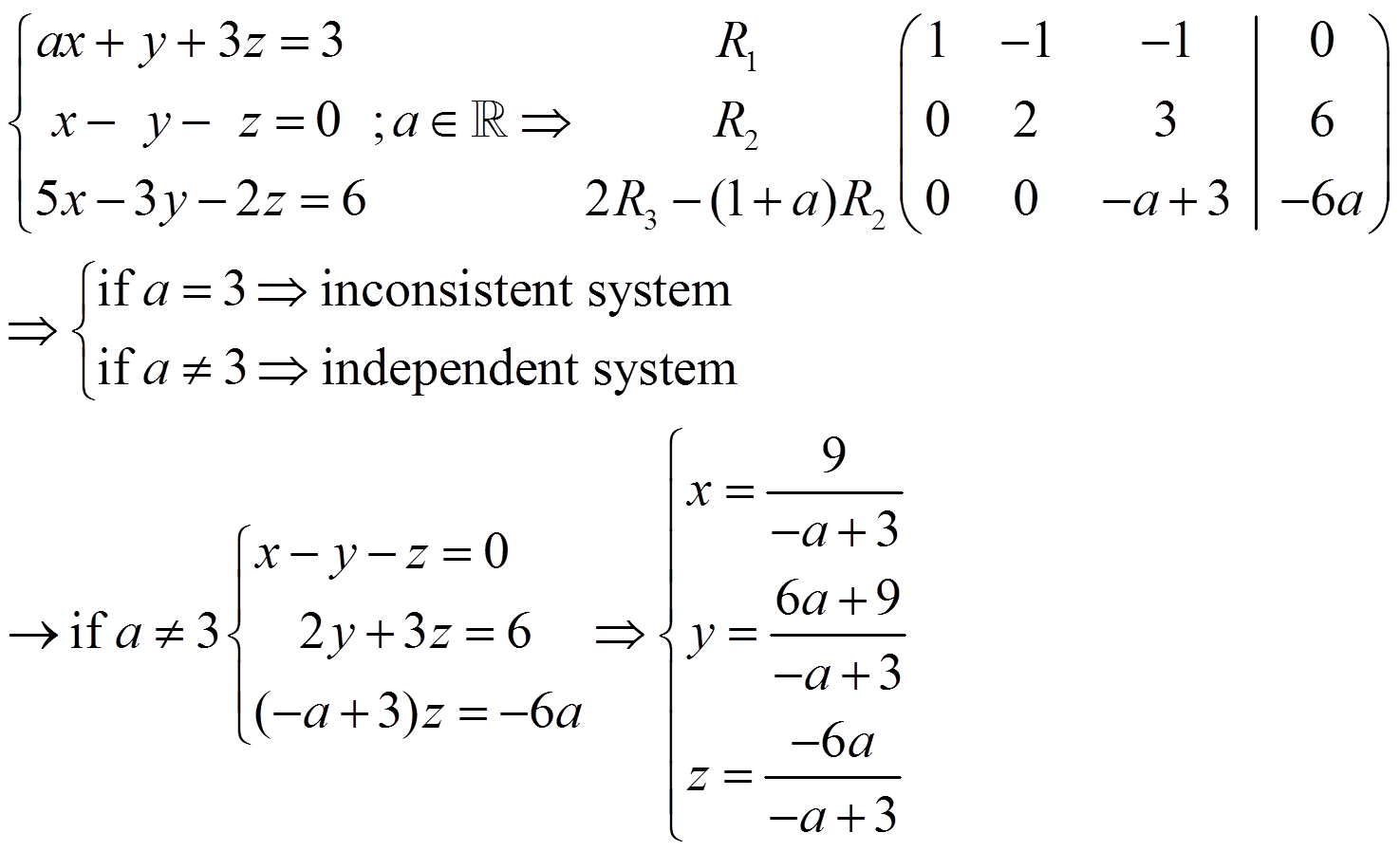
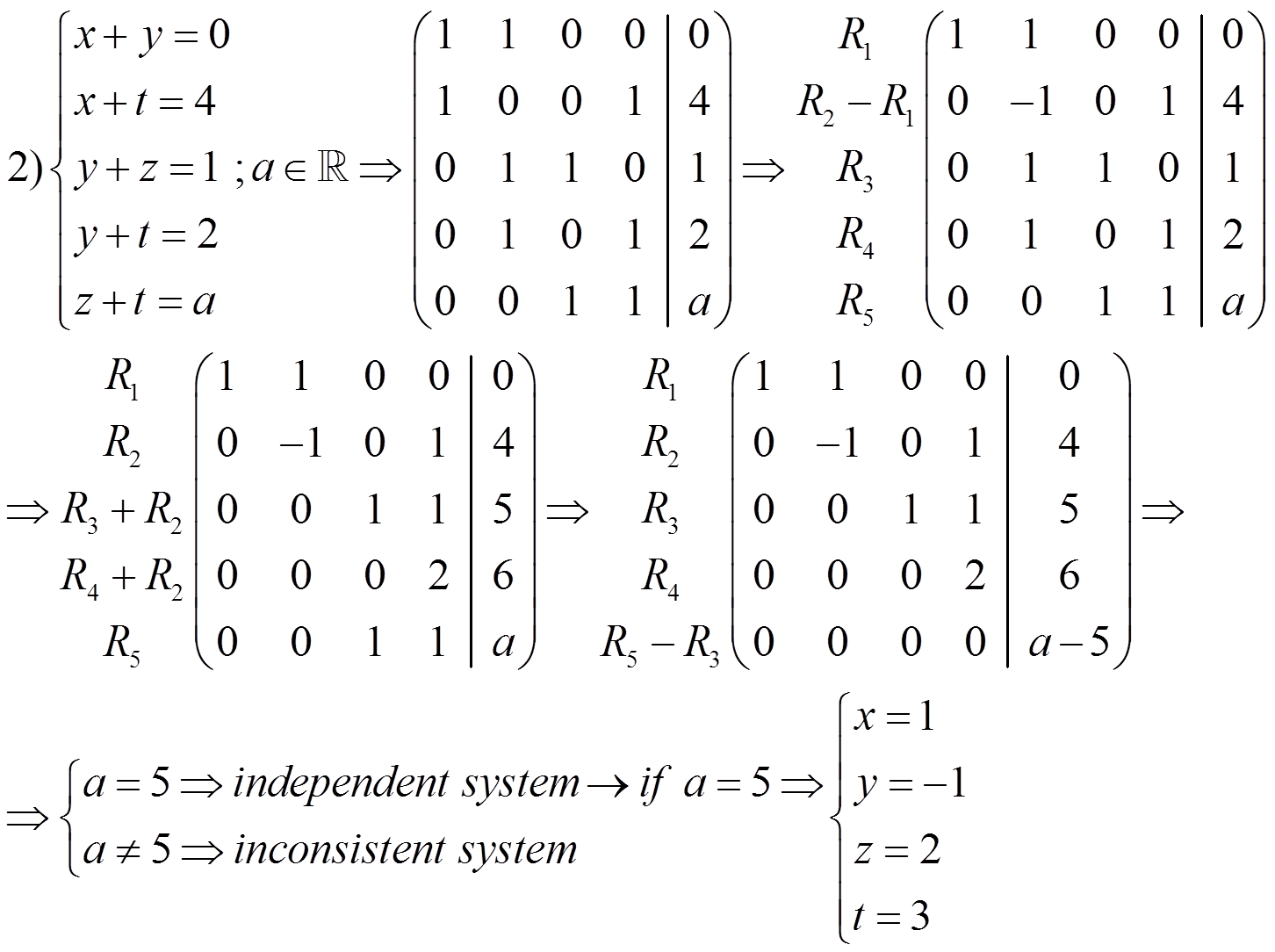
Exercises: discuss and solve the following systems:
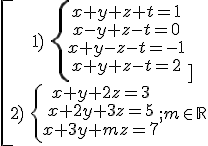
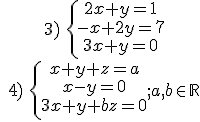
Solutions:
1) independent system:x = -1, y = 1, z = 3/2, t = -1/2
2) m ≠ 4 independent system: x = 1, y = 2, z = 0
m = 4 dependent system: x = 1 - λ, y = 2 - λ, z = λ; λ€R
3) independent system: x = -1, y = 3
4) b ≠ 2 independent system: x = y = ab/(2b-4), z = -2a/(b-2)
b = 2 and a = 0 dependent system: x = y = λ, z = -2λ; λ€R
b = 2 and a ≠ 0 inconsistent system
Licensed under the Creative Commons Attribution Non-commercial Share Alike 3.0 License