SystemsOfEquationsGaussianElimination
Systems of equation
A polynomial equation of degree 1 with one or several unknowns is called a linear equation:
![]()
All the linear equations have this form:
a1x1 + a2x2 + …..+ anxn = b
where a1,a2,…, an,b are real numbers and x1, x2, ….., xn are unknowns or variables
If b = 0 it is called a homogeneous equation.
A solution of the equation is a set of values of the variables, x1 = k1, x2 = k2,…., xn = kn, which converts the equation into a numerical equality.
Examples:
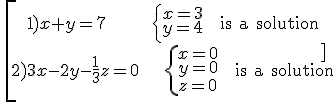
A system of m linear equations with n unknowns is a set of m linear equations with n unknowns given together with the target of determining the common solution/s of all of them. It has the form:
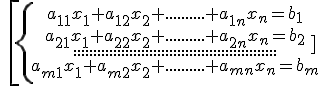
Where x1,x2,…….xn are the variables and aij, bi are real numbers, i = 1,2….m, j = 1,2,….n
Examples:
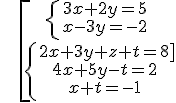
Licensed under the Creative Commons Attribution Non-commercial Share Alike 3.0 License