Real Numbers
As we said before, there are numbers that we can’t express as the quotient of other two numbers as: π = 3.1415.., e = 2.7182.. , √2 = 1.4142.., golden ratio = Ψ =(1+√5)/2 = 1.61803..
These numbers are called Irrational Numbers, and if we add them to the Rational Numbers we obtain the Real Numbers, R , which we can represent in a straight line. This line is called the real number line:
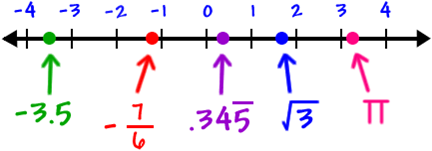
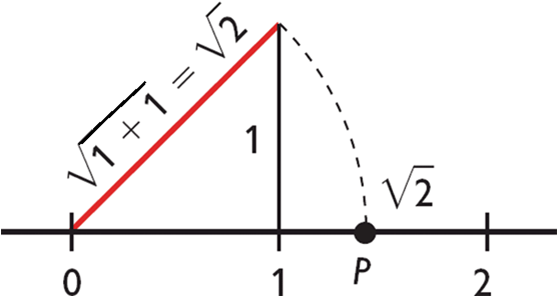
Now, we have these sets of numbers:
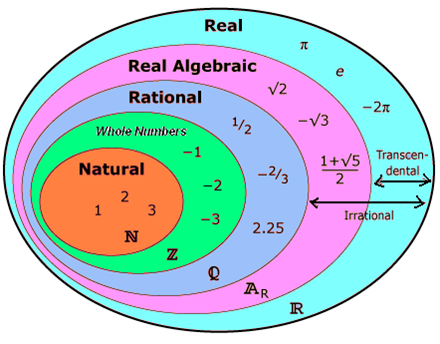
Exercises:
1.- Classify these numbers:
a) 121/11
b) 1.234567....
c) -√225
d) -1/7
Solutions: a) N; b) R; c) Z; d) Q
2.- Represent these numbers in the real number line: √29, √41
3.- True-False Question
Decide if the following sentences are true or false:
a) All Natural Numbers are Real Numbers
b) All Natural Numbers are Irrational Numbers
c) All Rational Numbers are Whole Numbers
d) All the Decimal Numbers are Rational Numbers
Obra colocada bajo licencia Creative Commons Attribution Non-commercial Share Alike 3.0 License