Complex Numbers

There are situations in which Real Numbers are not enough, for example when we solve a quadratic equation and we find the square root of a negative number.
To solve these problems, we define the imaginary unit or unit imaginary number “i” as a number such that

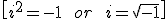
Now we can solve negative square roots:

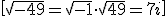
Or solve all the quadratic equations:

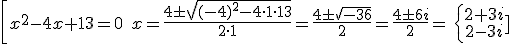
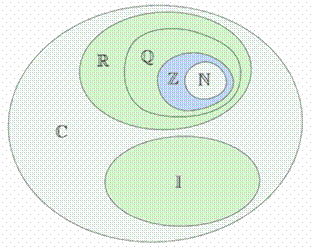
Then the Complex Numbers set is:

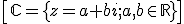
Examples: 2-7i, 3+πi, -20i, 157’28-i, 1428

  a + bi is called binomial form of a complex number. a is called real part and b imaginary part.

  Now, we have these sets of numbers:

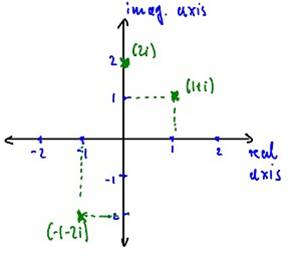
  We can represent the Complex Numbers in the plane: