operations with Complex Numbers
Two complex numbers are equal if they have the same real and imaginary part.
To add or subtract complex numbers, we add or subtract their real and imaginary parts:
(3 + 2i) + (7 – i) = 10 + i
To multiply complex numbers, we have to remember that i2 = -1:
(3 + i) · (2- 2i) = 6 + 2i – 6i – 2i2= 8 – 4i
(1 + 3i)2 = 12+(3i)2+2·1·3i = 1 – 9 + 6i = -8 + 6i
The conjugate of z = a + bi is:
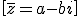
As you can check:
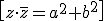
Then, to divide complex numbers, we multiply the denominator and the numerator by the conjugate of the denominator:
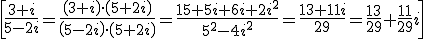
We use it to calculate the inverse of a complex number:
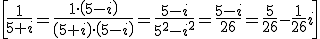
If we calculate the powers of i:
i1= i i2= -1 i3=i2·i= -i i4=i2·i2=(-1)·(-1)= 1 i5=i4·i= i i6=i4·i2= -1 ......
Then to calculate a power of i we only calculate the remainder of the division of the power by 4: i147=i3=-i
Exercise. If z=3+2i and w=1-i. Calculate:
a) z-3w=
b) z·w=
c) z2 =
d) 1/w=
e) z/w=
f) i78 =
g) z + i327 =
h) i433 ·i123=
Solutions:
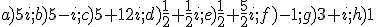
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 3.0