DerivativeApplications
8. inflection points and curvature
To study the curvature of a derivable function, you have to find the intervals in which the function is concave up or concave down.
f is concave up in c if the graph is above the tangent line to the curve in c.
f is concave down in c if the graph is under the tangent line to the curve in c.
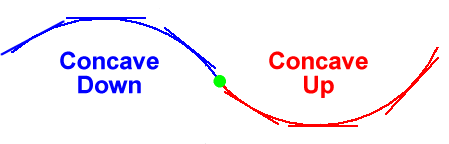
An inflection point is a point on a curve at which the curvature or concavity changes.
If f is derivable in (a,b)
– f is concave up in (a,b) ↔ f’’(x) > 0
– f is concave down in (a,b) ↔ f’’(x) < 0
If is derivable in cЄR, then:
- f has an inflection point in c → f’’(c) = 0

Exercise: study the curvature of the function y = x·ex and find its inflection points
Solutions: inflection point (-2, -2/e2); concave up (-2,∞); concave down (-∞,-2)
Licensed under the Creative Commons Attribution Non-commercial Share Alike 3.0 License