9. graph
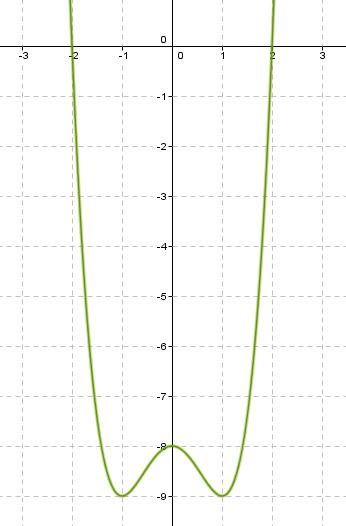
Example 1: f(x) = x4 + 8x3 + 22x2 + 24x + 9
•1. Domf = R
•2. f is continuous and derivable in R because it is a polynomial function.
•3. Symmetry: f is a function which is neither odd nor even.
•4. f is not a periodic function.
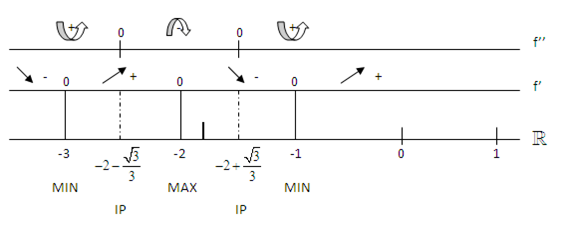
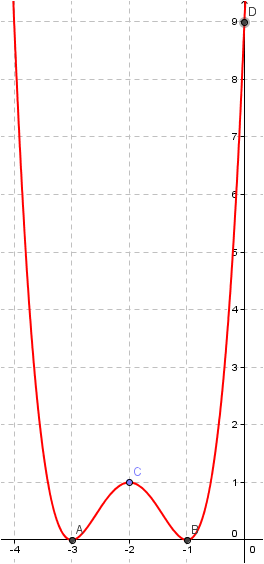
•5. intersection points: (-3,0),(-1,0),(0,9)
•6. There are no asymptotes because it is a polynomial function.
•7. f’(x) = 4x3 + 24x2 + 44x + 24 f’(x) = 0 ↔ x Є {-3, -2, -1}
Example 2: f(x) = x3 + 3x2 - 4
•1. Domf = R
•2. f is continuous and derivable in R because it is a polynomial function.
•3. Symmetry: f is a function which is neither odd nor even.
•4. f is not a periodic function.
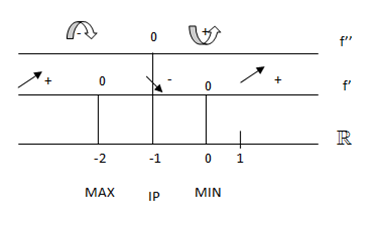
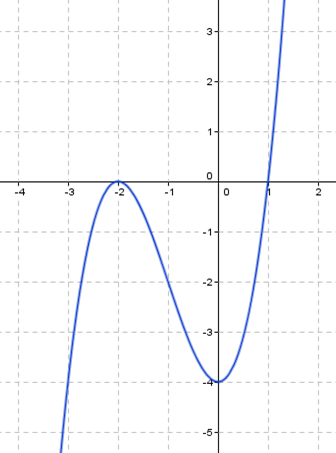
•5. intersection points: (-2,0),(1,0),(0,-4)
•6. There are no asymptotes because it is a polynomial function.
•7. f’(x) = 3x2 + 6x
f’(x) = 0 ↔ x Є {-2, 0}
f’’(x) = 0 ↔ x =-1
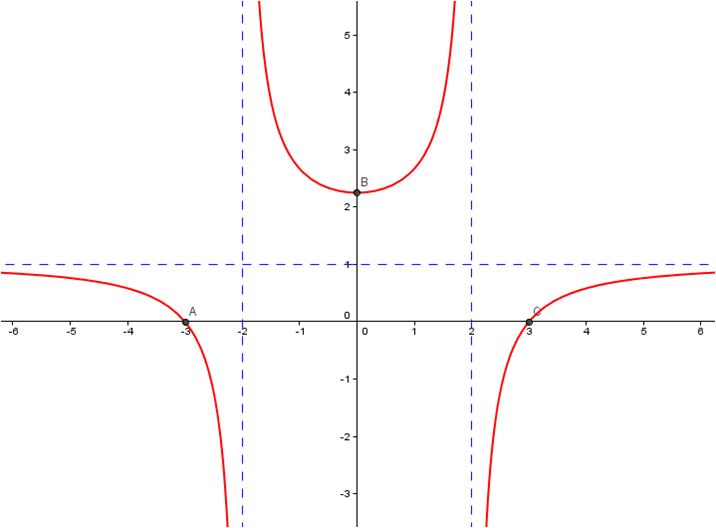
Example 3:
![]()
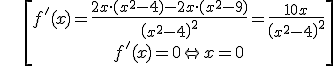
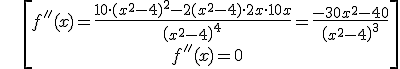 no solution
no solution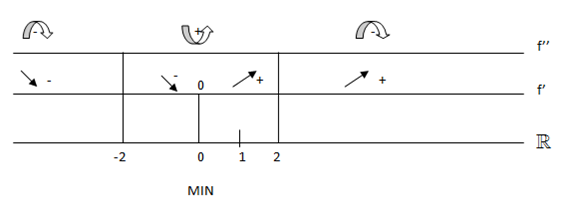
Licensed under the Creative Commons Attribution Non-commercial Share Alike 3.0 License