Angles and distances

The distance between two points, A(a₁,a₂) and B(b₁,b₂), is the magnitude of the vector AB:

 

The distance between a point and a straight line, A(a₁,a₂) and r:Ax + By + C = 0, is:

The distance between two parallel straight lines, r and s, is the distance between a point in one of them and the other line: d(r,s)=d(A,s)=d(B,r)

The angle between two straight lines, r and s, is:

Example:

 

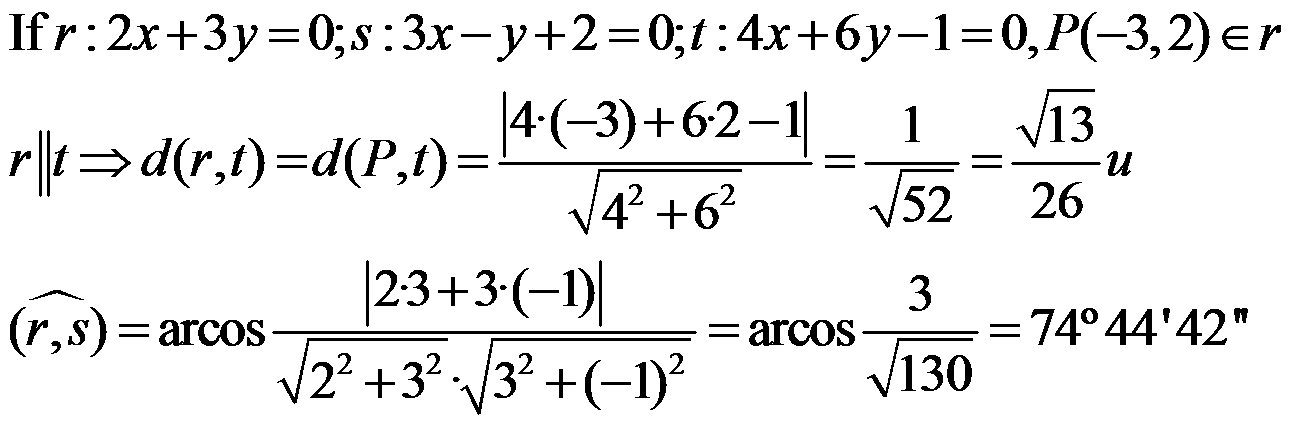
The coordinates of the middle point of a segment AB, where A(a1,a2) and B(b1,b2), is:

 

Exercises:

1.- Calculate the middle point of the segment AB, where A(1,1), B(3,8)

2.- If A(3,3), r: x + 3y + 7 = 0; s: 2x + 6y + 7 = 0; t: 2x - y = 0; calculate:

a) d(A,r)

b) d(r,s)

c) The angle between r and t

 

 

 

 

Solutions: 1.- M(2,9/2); 2.- a) 6u; b) 1.1u; c) 98º7'48''