Straight line equations
The direction vector for a line is any vector with the same direction as the straight line.
To determine a straight line and its equations, we need to know one point and a direction vector or two points (to obtain a direction vector).
If we have a point, A(a1,a2), and a direction vector, u(u1,u2), of a straight line r, then any point X Є r, has a position vector X(x,y):
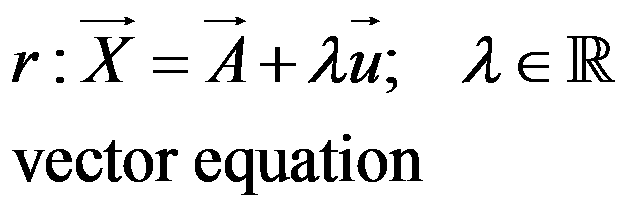
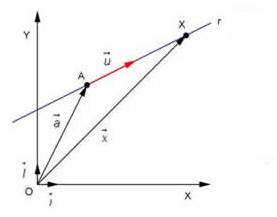
In coordinates:
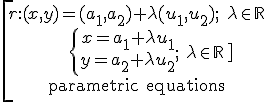
If we work out λ:
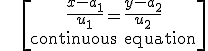
By doing the cross-product and simplifying:
![]()
The slope or gradient of a straight line, m, is the tangent of the angle that the line and the abscissa axis form : m = tan α
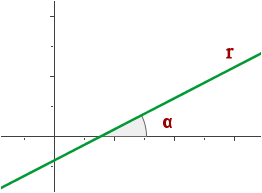
You can see that:
![]()
Then, a straight line can be determined too, if we know a point and the slope:
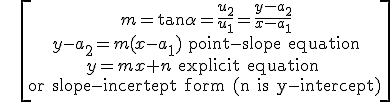
NOTE:
![]()
Example: find out all the equations of a straight line that passes through the point A(1,1) in the direction of the vector u(-3,2).
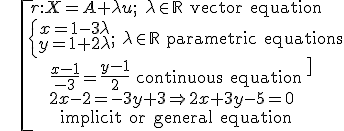
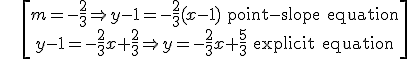
Exercises:
1.- Find out all the equations of a straight line that passes through the point (3,-1) and has the direction of the vector (-1,1).
2.- Find the other equations of the straight line r: y = 3x + 2
Solutions:
1.-
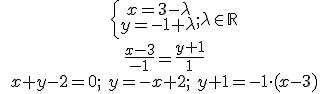
2.-
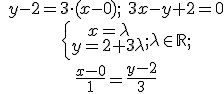
Licensed under the Creative Commons Attribution Non-commercial Share Alike 3.0 License