Relative position of two lines

Two straight lines, r and s, can be:
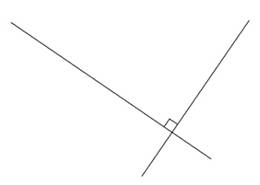
- Intersecting lines, if they intersect at a point. If the angle they form is 90⁰, they are perpendicular.

         

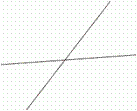
- Coincident lines, if they contain the same points.

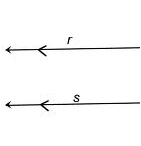
- Parallel lines, if there aren’t any intersection points.

Case 1: we know a point and a direction vector of each straight line: r {A,u}; s {B,v}

-If u and v are linearly dependent:
      · If u and AB are linearly dependent, r and s are coincident lines.
      · If u and AB are linearly independent, r and s are parallel lines.
- If u and v are linearly independent: r and s are intersecting lines.

Example:

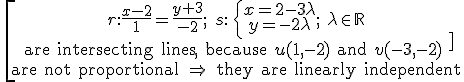
Case 2: we know a point and the slope of each straight line: r {A,m_r}; s {B,m_s}

- If m_r = m_s:
      · If A Є s, r and s are coincident lines.
      · If A ¢ s, r and s are parallel lines.
- If m_r ≠ m_s: r and s are intersecting lines.

Example:

Case 3: we know the implicit equations of the lines: r :Ax + By + C = 0; s:A’x+ B’y+ C’ = 0

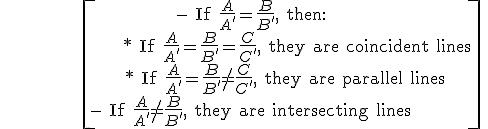
Example:

 

 

Exercise: Determine the relative position of these pairs of straight lines:

a) 3x + 3y - 5 = 0; 6x + 6y -11 = 0

b) y = 3x + 2 ; y - 3 = 2·(x+1)

c) x = 1 + λ

    y = 3 -3λ  , λ€R ;         y = 3x + 2

d) 3x - 3y - 15 = 0; y + 2 = 1·(x - 3)

 

 

Solutions: a) parallel; b) intersecting; c) intersecting; d) coincident