discontinuities

There are different kinds of discontinuities:

- Removable discontinuity: if the limit exists and it is not equal to f(a).
Example 1:

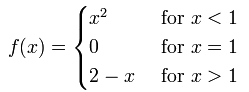
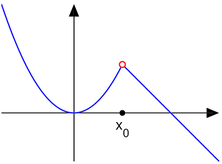
                                                                                           f has a removable discontinuity in x = 1

- Jump discontinuity: when the lateral limits exist and they are not equal. The jump can be finite or infinite.
Example 2:

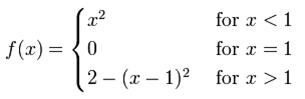
                                                                    f has a jump discontinuity in x = 1, with jump 1.

Example 3:

 

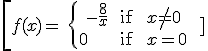
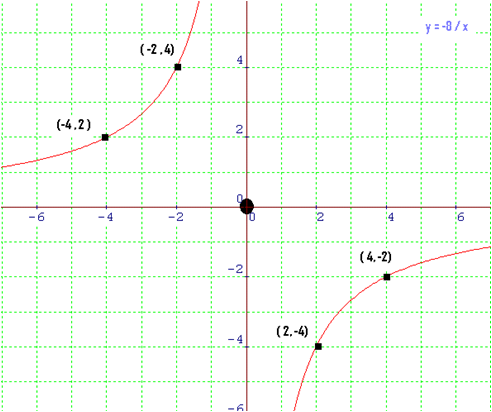              f has an infinity jump discontinuity in x = 0

- Essential discontinuity: when one of the lateral limits does not exist.
Example 4:

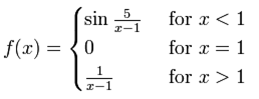
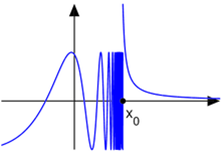
does not exist  

 

 

Exercise: study the continuity of these functions and classify their discontinuities if they have them:

 

 

 

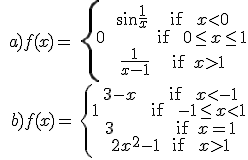
Solution: a) f is continuous in R-{0,1}, in x = 0 f has an essential discontinuity and in x = 1 f has an infinity jump discontinuity

             b) f is continuous in R-{-1,1}, in x = -1 f has a jump discontinuity, with jump 3, and in x = 1 f has a removable discontinuity