limit of a sequence

The sequence is said to converge if there exists a number L such that no matter how close we want the a_n to be to L, we can find a natural number k such that all terms {a_k, a_k+1, ...} are as close to L.

Then it is said that the sequence is convergent and L is its limit,     

Otherwise, it is said that the sequence is divergent.

Examples:
·        is convergent and  

·      diverges and 

·     is an oscillating sequence and does not exist 

Properties:

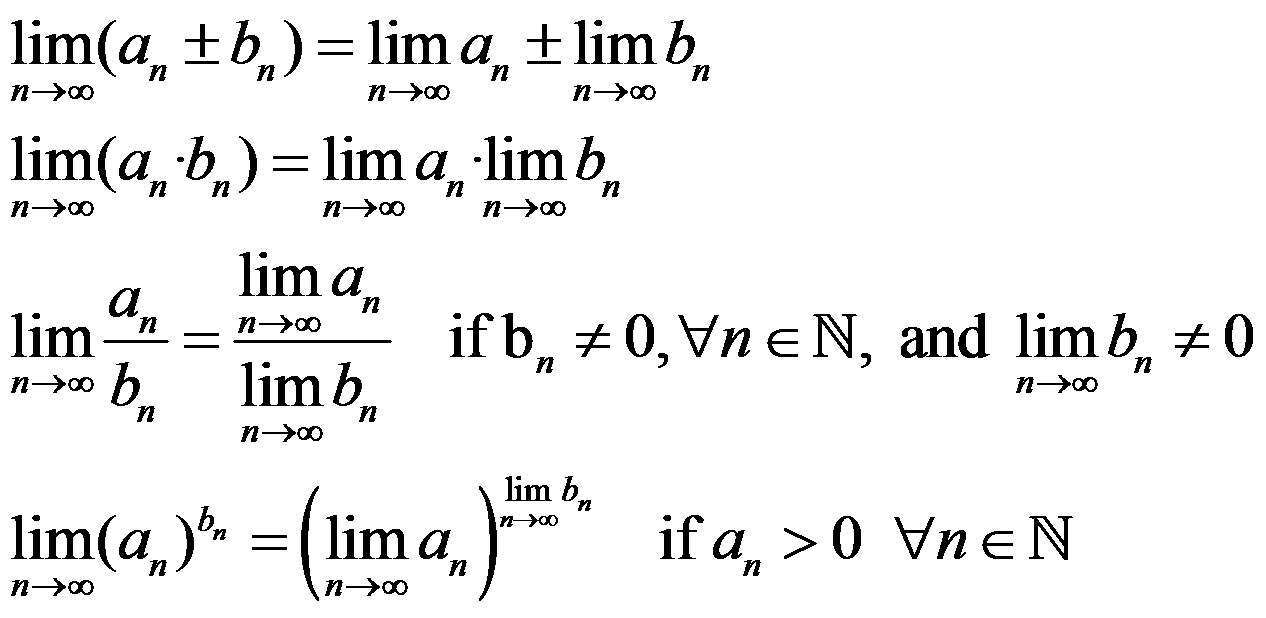
Note:

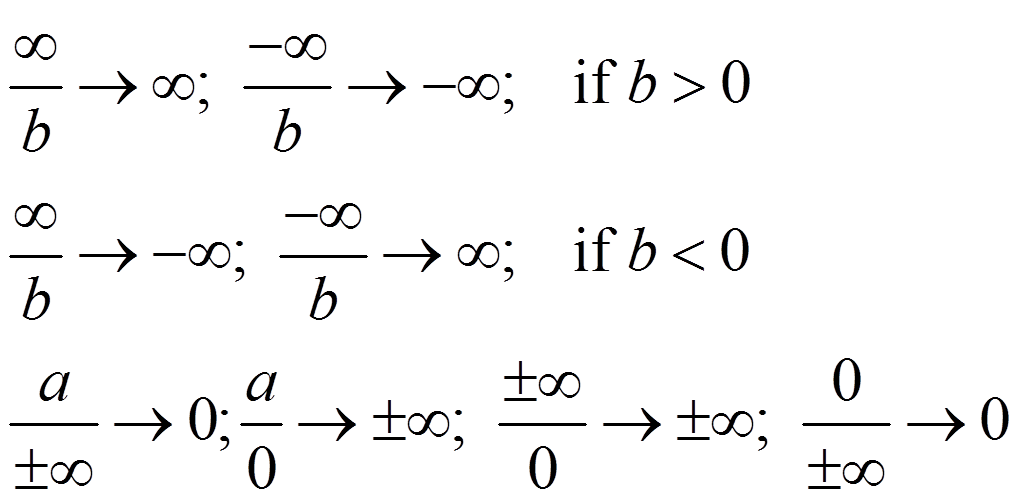
Examples:

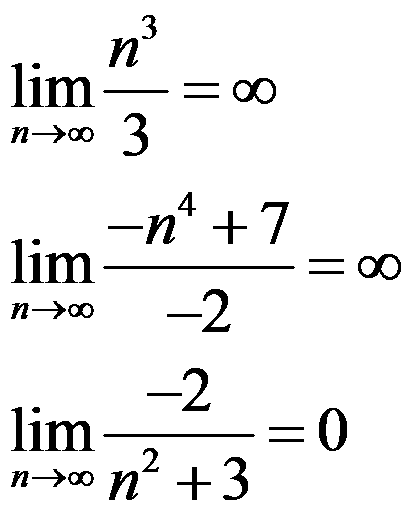
Exercise: calculate:

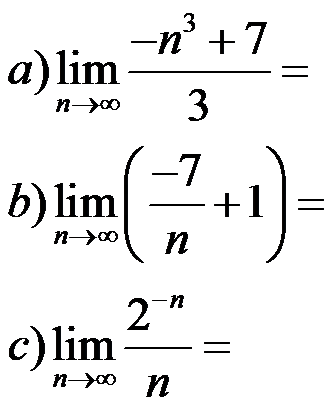
Solutions: a) -∞; b) 1; c) 0