Limits of functions

The limit of function f as x approaches c is L if f(x) can be made to be as close to L as desired by making x sufficiently close to c. Otherwise:

We write:

For example:

  

because:          

You can't always find the same limit when you approach from both sides, that’s why we define the lateral or one-sided limits:

- The limit of a function f as x approaches c from the left is L^- if f(x) can be made to be as close to L^- as desired by making x sufficiently close to c from below:

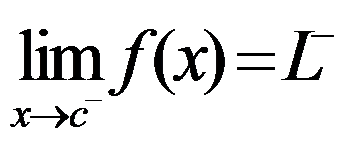
- The limit of a function f as x approaches c from the right is L⁺ if f(x) can be made to be as close to L⁺ as desired by making x sufficiently close to c from above:

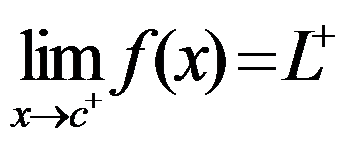
For example:

 

Then, the function has a limit on c if and only if the one-side limits exist and are equal:

Then, in the example

We have the same properties as in the sequences:

 

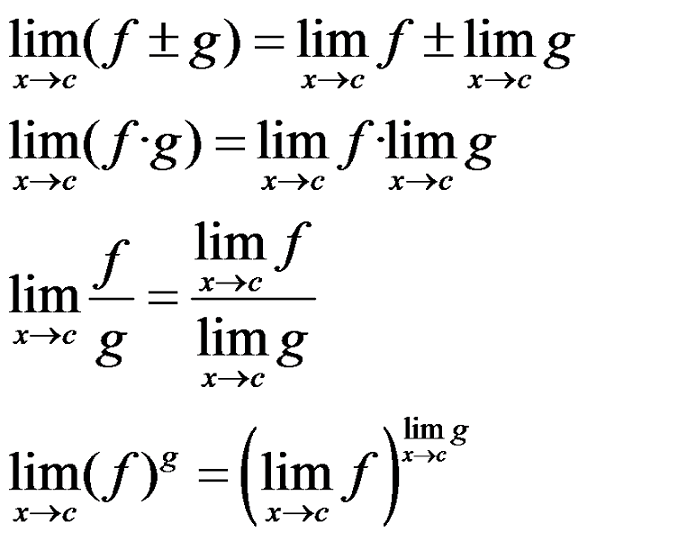
Exercise: calculate the limit of f as x approaches -1, 2 and 5, if:

 

 

 

 

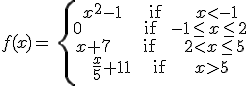
Solutions: