Cramer's rule

We say a system is a Cramer’s system if:

(1) # equations = # unknowns

(2) det A ≠ 0

Then

(i) It is an independent system

(ii)    where A_i is the resultant matrix when we change the i^th column for B

Example 1:

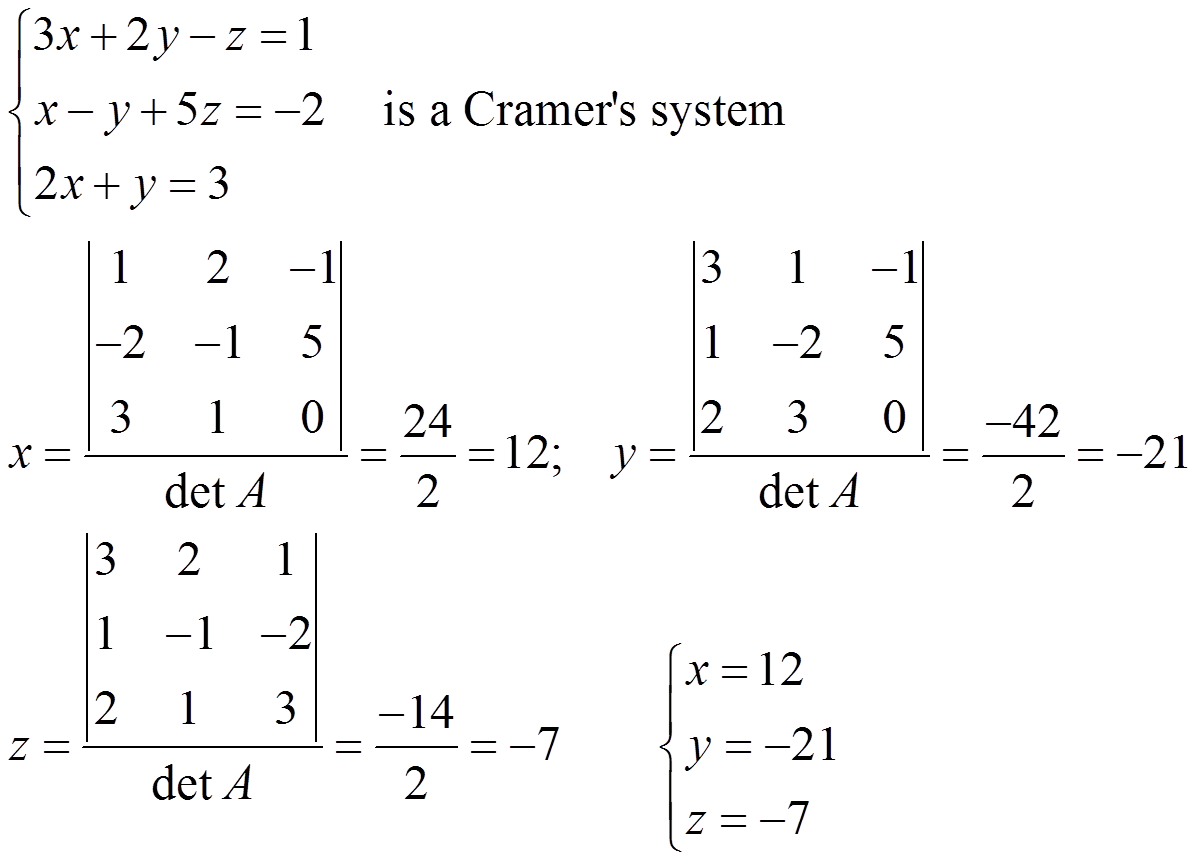
Example 2:

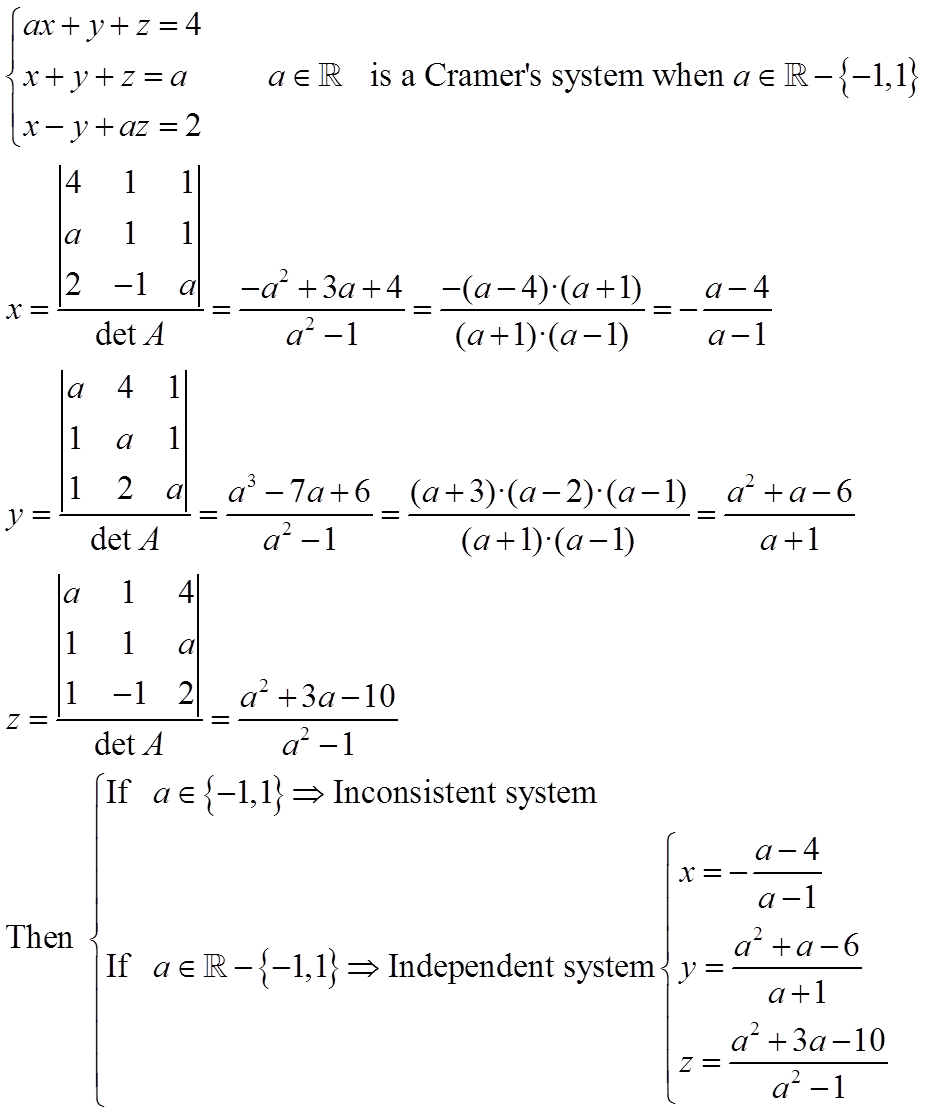
Exercise: solve the following systems by using Cramer's rule, when they are consistent:

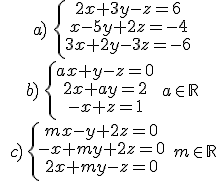
Solutions:

a) x = 1; y = 3; z = 5

b) If a = 2; x = -1 + λ; y = 2 + λ; z = λ; λ € R

     If a € R-{-1,2}; x = 1/(a+1); y = 2/(a+1); z = (a+2)/(a+1)

c) If m ≠ -1; x = y = z = 0

    If m = -1; x = y = z = λ € R