Rank

Let A € Mmxn(R) , it is called minor of order p to the determinant of each submatrix pxp of A.

Then, the rank of A is the largest order of any non-zero minor in A.

Likewise, it is said that a row or column is linearly dependent if it is a linear combination of the others. Otherwise, it is called linearly independent. Then, the rank of a matrix is the size of the largest collection of linearly independent columns (or rows) of A.

There are two different ways to calculate the rank of a matrix:
 
–Gauss: we get the row echelon form of a matrix and the rank is the number of non-zero rows or columns.
 

Example 1:

–Minors. Example 1:
 

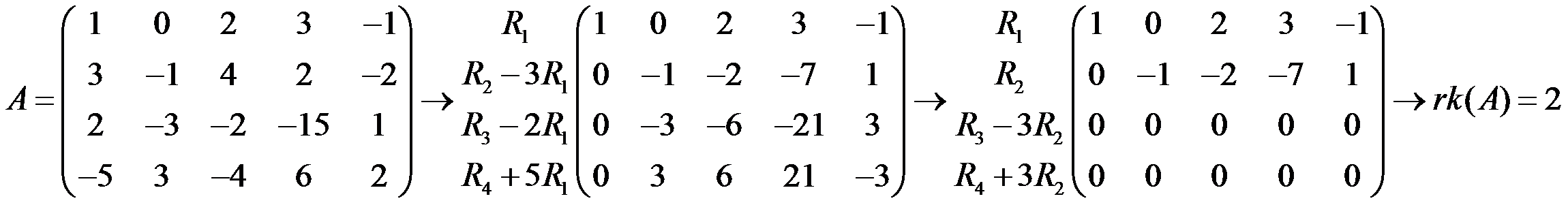
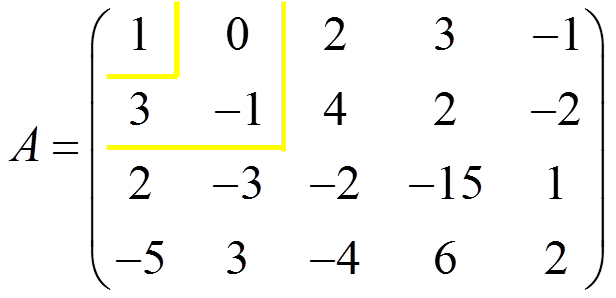
We look for non-zero determinant of order 1:

                |1|≠ 0

Then a non-zero determinant of order 2, with the determinant of order one inside:

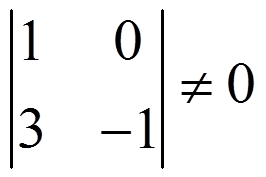
We edge the determinant of order 2 with the third row:

               

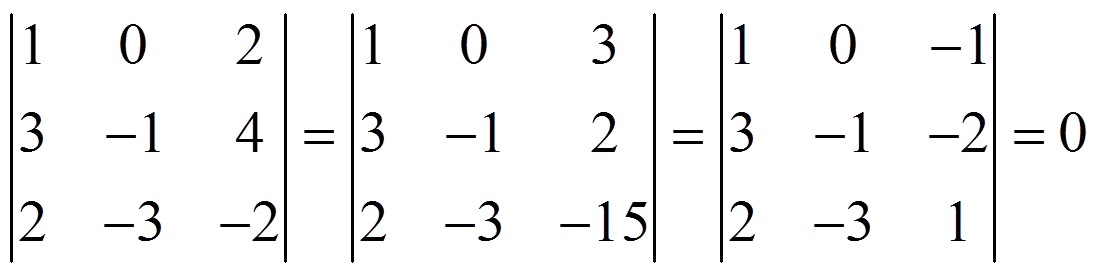
As all of them are zero, we remove the third row, because is linearly dependent:

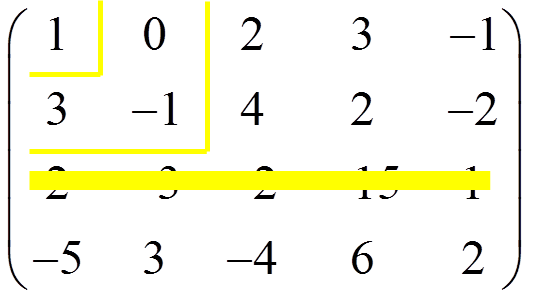
We do the same with the fourth row

               

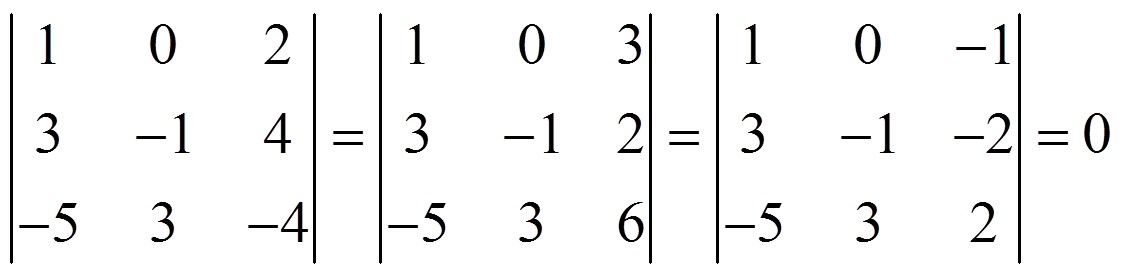
As all of them are zero, we remove the fourth row → rank(B) = 2

 

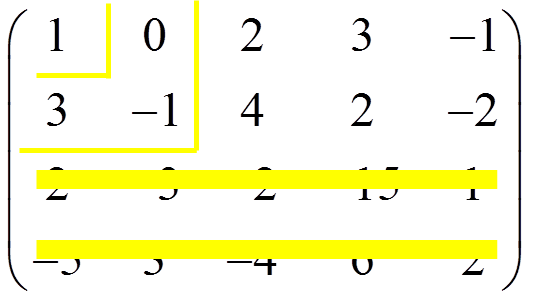
NOTE: in the beginning, we must remove the rows or columns of zeros, equal or proportional

Example 2:


               

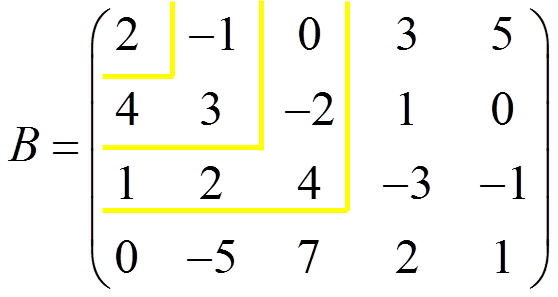
We have a non-zero determinant of orders 1 and 2, and we edge this last one:

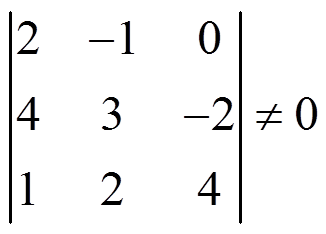
Then we edge this determinant with the fourth row:

 

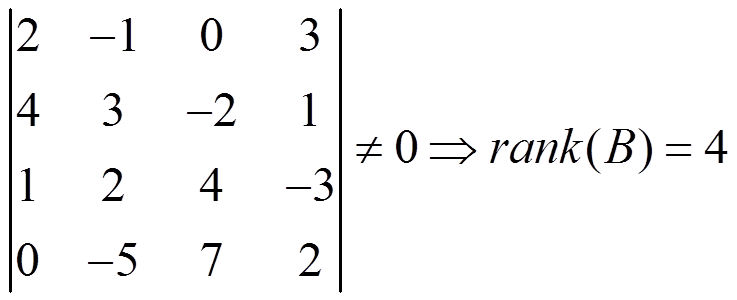
Exercises:

1.- Calculate the rank of the matrix:

 

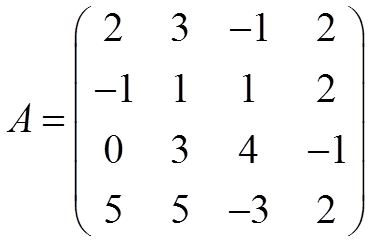
2.- Calculate the rank of the following matrices depending on the value of a:

 

 

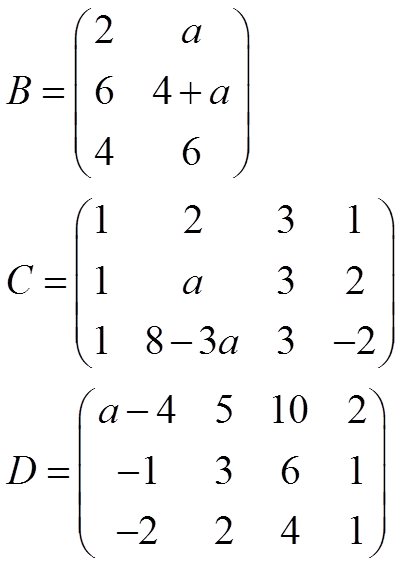
Solutions: 1) rank(A) = 3

2) rk(B) = 1 if a = 2; rk(B) = 2 if a ≠ 2

rk(C) = 2     a € R

rk(D) = 2 if a = 1; rk(D) = 3 if a ≠ 1

Licensed under the Creative Commons Attribution Non-commercial Share Alike 3.0 License