Relative positions

A. TWO PLANES

- If rk(A)=rk(A*)=1 → coincident planes

- If rk(A)=1≠2=rk(A*) → parallel planes

- If rk(A)=rk(A*)=2 → intersecting planes

 

Example 1:

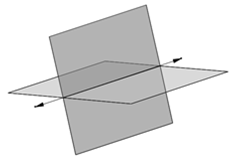
  rk(A)=1≠2=rk(A*) → parallel planes

Example 2:

  rk(A)=rk(A*) =2 → intersecting planes

 

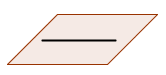
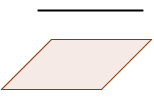
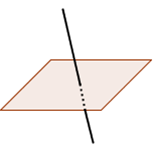
B. A PLANE AND A STRAIGHT LINE

- If rk(A)=rk(A*)=2 →  straight line into the plane
 
 
- If rk(A)=2≠3=rk(A*) → parallel ones
 
 
- If rk(A)=rk(A*)=3 → intersecting ones
 
 
 

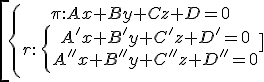
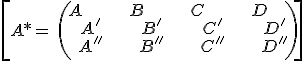
Example 3:

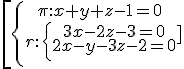
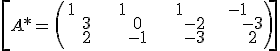
rk(A)=rk(A*)=2 → line into the plane

 

Example 4:

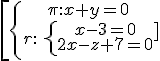
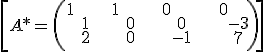
rk(A)=rk(A*) =3 → intersecting ones

 

C. TWO STRAIGHT LINES

 

- If rk(A)=rk(A*)=2 →  coincident lines
 
 
- If rk(A)=2≠3=rk(A*) →  parallel lines
 
 
 
- If rk(A)=rk(A*)=3 → intersecting lines
 
 
- If rk(A)=3≠4=rk(A*) → skew lines
 
 

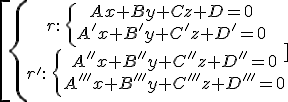
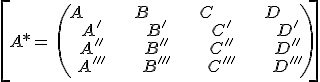
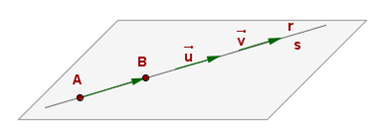
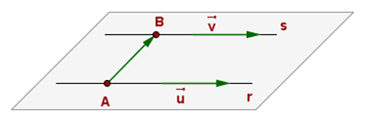
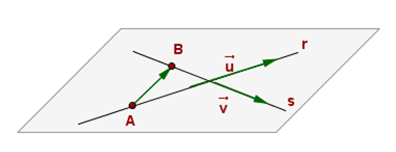
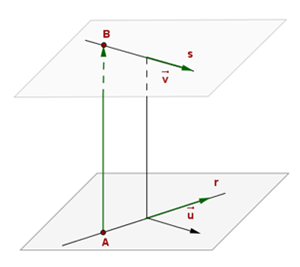
Example 5:

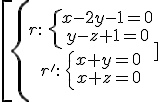
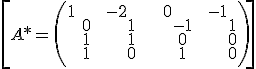
rk(A)=3≠4=rk(A*) → skew lines

Example 6:

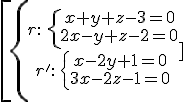
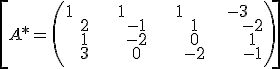
rk(A)=rk(A*) =3 → intersecting ones

 

D. THREE PLANES

 

 

- If rk(A)=rk(A*)=1 → coincident planes
 
 
- If rk(A)=1≠2=rk(A*) → Two coincident and one parallel or three parallel planes

  

- If rk(A)=rk(A*)=2 → Either they intersect at a line or there are two coincident and the other intersects at a line
 
 

- If rk(A)=2≠3=rk(A*) → Either there are two parallel ones and another one intersecting or they form a triangular prism
 
  

- If rk(A)=rk(A*)=3 → They intersect at a point
 
 
Example 7:
 

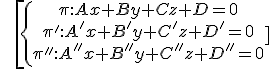
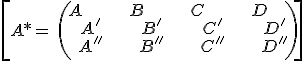
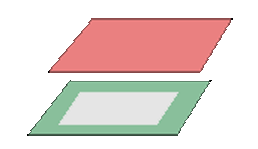
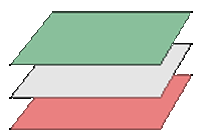
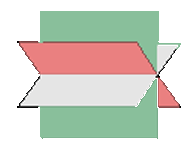
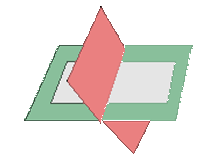
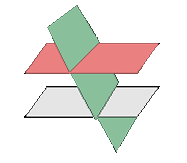
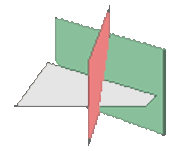
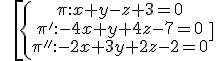
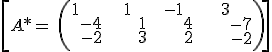
  rk(A)=2≠3rk(A*)→ they from a prism

Example 8:
 


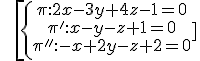
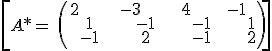
  rk(A)=rk(A*) =3 → intersecting ones

 

 

Exercises:

1.- Study the relative position of the plane π: x + 2y - 1 = 0 and the straight line r:

 

2.- Study the relative position of the lines r and s, where:

 

 

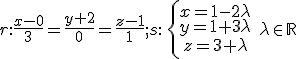
Solutions: 1) Parallel ones; 2) Intersecting lines

Obra colocada bajo licencia Creative Commons Attribution Non-commercial Share Alike 3.0 License