Primitive Calculus
Indefinite integral
Let f a function, it is said that F is a primitive of f if F’ = f.
NOTE: if F is a primitive of f → F + k (k Є R) is a primitive of f.
The indefinite integral of f is the set of primitives of f:
![]()
Example: 1) ∫cosx dx = sinx + k; k Є R
PROPERTIES:
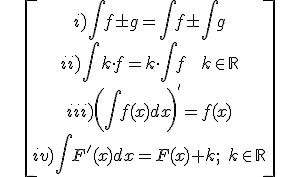
Examples:
2) ∫3sinxdx =3 ∫sinxdx = -3cosx + k k Є R
3) ∫(ex+3)dx = ex + 3x + k k Є R
Exercise. Solve:
a) ∫3x2 dx =
b) ∫2sinx·cosx dx =
Solutions: a) x3 + k; b) sin2x + k
Licensed under the Creative Commons Attribution Non-commercial Share Alike 3.0 License