Primitive Calculus
Integration of rational functions
![]()
I) If degP ≥ degQ, we have to divide and decompose:
![]()
q(x) = quotient; r(x) = remanider
Then we have: polynomial + immediate integral or case II
II) If degP < degQ, we have three cases:
- Q only has simple real roots
- Q has multiple real roots
- Q has complex roots
II.a) Q(x) = a·(x – x1)·(x – x2)·…
Then, we have to look for A1, A2,…Є R, such that:
![]()
and we have immediate integrals (ln)
Example:
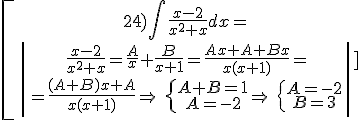
![]()
II.b) Q(x) = (x – x1)n ·…
Then, we have to look for A1, A2,…,AnЄ R, such that:
![]()
and we have immediate integrals, again
Example:
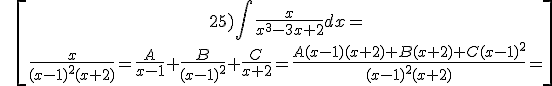
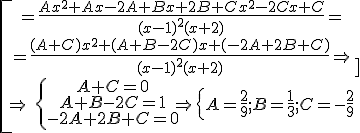
![]()
II.c) Q(x) = (ax2 + bx + c)·…
Then, we have to look for M,NЄ R, such that:
![]()
and we have immediate integrals (ln + arctan)
Example:
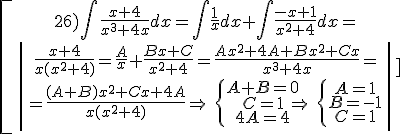
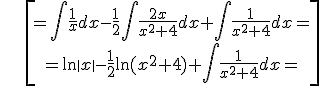
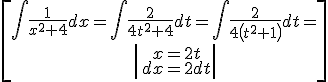
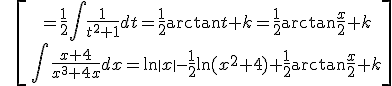
Exercise. Solve the following integrals:
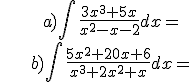
Solutions:
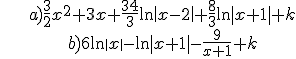
Licensed under the Creative Commons Attribution Non-commercial Share Alike 3.0 License