∫u dv = u·v - ∫v du

Demonstration: There is a formula for the differentials analogue to the formula of the derivatives (u·v)’ = u·v’ + u’·v

d(u·v) = du · v + u · dv

then if we integrate it

∫d(u·v) = ∫v du+∫u dv and if we work out:

∫u dv = u·v - ∫v du  QED

Examples:

 

 

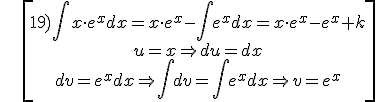
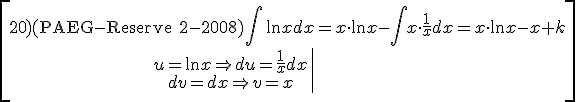
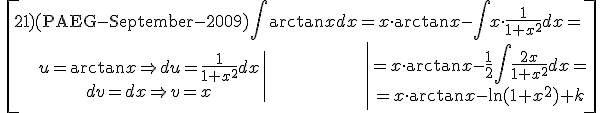
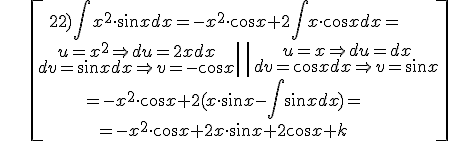
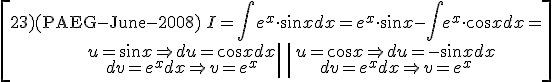
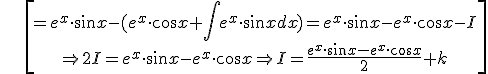
 Exercise. Solve the following integrals:

a) ∫x·cosx dx =

b) ∫x³e^x dx =

 

 

 

 

Solutions: a) x·sinx + cosx + k; b) e^x(x³ - 3x² + 6x -6) + k