ratios in a circumference

If P(x,y) is the intersection point of the circumference of radius r and the radius that makes the angle, then: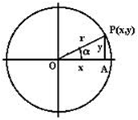

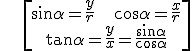
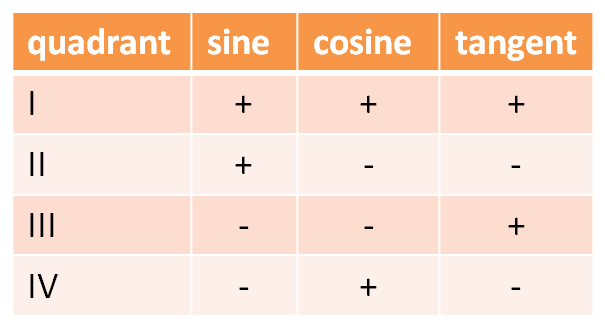
The sign of the ratios in the quadrants are:

Properties:
· sin² α + cos² α = 1, because of the Pythagorean Theorem.
· tan² α + 1 = sec² α, if we divide the above formula by cos² a
·    - 1 ≤ sinα ≤ 1       -1 ≤ cosα ≤1

With these properties, we can calculate all ratios if we know one of them:
Example: if sin α = 0,6 and α € II quadrant, find the other ratios. 

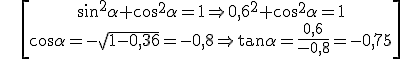
Exercises:

1.- Calculate the other ratios of these angles:

a) cosα = 5/13 and α € IV quadrant

b) tanβ = -3/4 and β € II quadrant

2.- Check these identities:

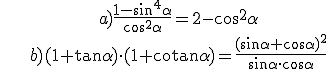
Solutions: 1.- a) sinα = -12/13, tanα = -5/12; b) sinα = 3/5, cosα = -4/5