Trigonometric ratios
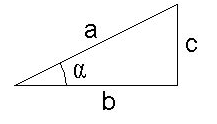
If we have a right-angled triangle, and one of its acute angles is a, then we define its sine, cosine and tangent as:
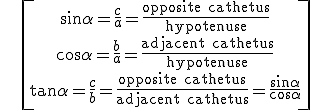
And their inverse ratios, cosecant, secant and cotangent:
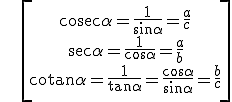
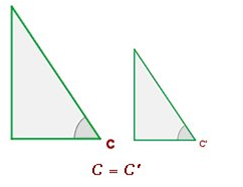
If you apply Thales’ Theorem, you can check that the ratios don’t depend on the lengths of the sides:
 |
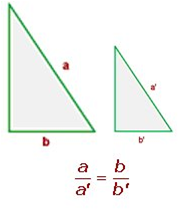 |
Example: 45o
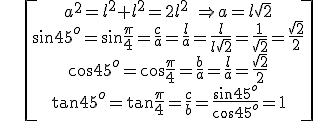
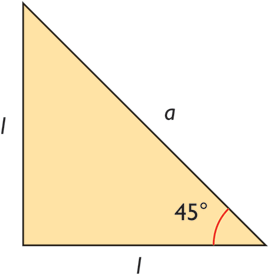
Exercises:
1.- Calculate the following trigonometric ratios:
a) sin 15o 45' 40''
b) tan 191o 15' 12''
2.- Calculate the angles knowing that:
a) sin α = 0,37
b) cos β = 0,8
3.- In a right-angled triangle, the catheti measure 3 and 4 and the hypotenuse measures 5. Calculate the ratios of its acute angles.
Solutions:
1.- a) 0,27; b) 0,198
2.- a) 21o 42' 56''; b) 38o 39' 35''
3.- sinα = cosβ = 3/5; cosα = sinβ = 4/5; tanα = cotanβ = 3/4
Licensed under the Creative Commons Attribution Non-commercial Share Alike 3.0 License