Trigonometric equations

A trigonometric equation is an equation with an unknown in a trigonometric ratio.

For example:  cos2x = sinx

To solve it, we have to follow these steps:

1. Apply the formulas and transformations to leave only one angle:
cos² x – sin² x = sinx

2. Use the formulas to get only one trigonometric ratio:
1 – sin² x - sin² x = sinx

3. Solve the equation as if the trigonometric ratio was the unknown:

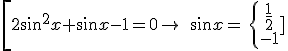
4. Calculate the angle with the help of a picture:

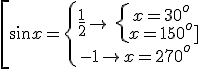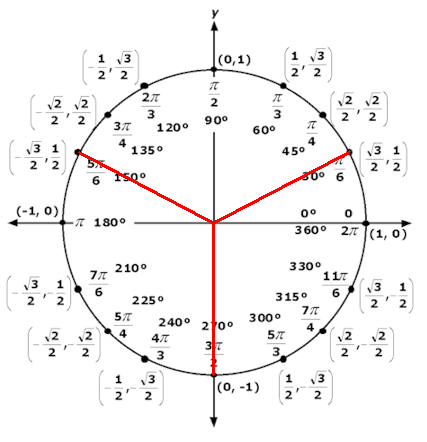5. Write the solutions by adding a whole number of circumferences. If the angle is a function of x, work out the unknown.

 

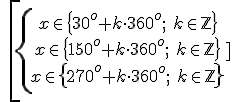
Exercise: Solve the following equations:

a)  sin 2x = tanx

b) sinx + sin2x + sin3x = 0

c) tanx · secx = √2

d) 2sin⁴x - 7cos²x + 3 = 0

 

 

Solutions:

a) x €{45^o + k90^o, k€Ζ}

b) x €{k90^o, k€Ζ}, x €{120^o + k360^o, k€Ζ}, x €{240^o + k360^o, k€Ζ}

c) x €{45^o + k360^o, k€Ζ}, x €{135^o + k360^o, k€Ζ}

d) x €{45^o + k90^o, k€Ζ}