Limit of a function

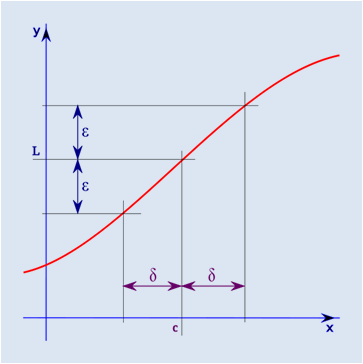
The limit of function f as x approaches c is L if f(x) can be made to be as close to L as desired by making x sufficiently close to c:

Or:

For example:

 because:

You can’t always find the same limit when you approach from both sides, that’s why we define the lateral or one-side limits:

–The limit of a function f as x approaches a from the left is L- if f(x) can be made to be as close to L- as desired by making x sufficiently close to a from below:

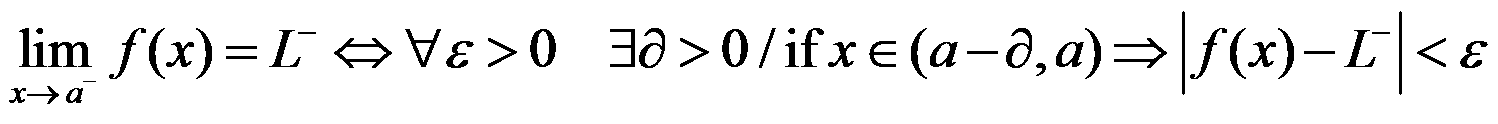
–The limit of a function f as x approaches a from the right is L+ if f(x) can be made to be as close to L+ as desired by making x sufficiently close to a from above:

For example:

Then, the function has a limit on a if and only if the one-side limits exist and are equal:

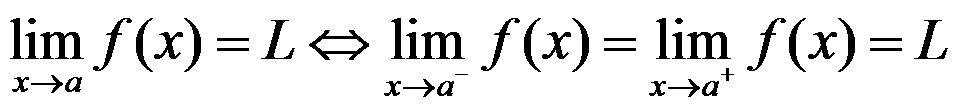
Then, in the example  

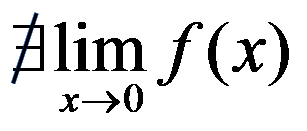
Other definitions:

 

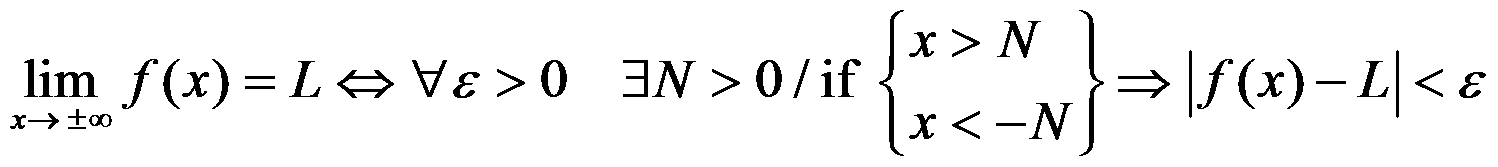
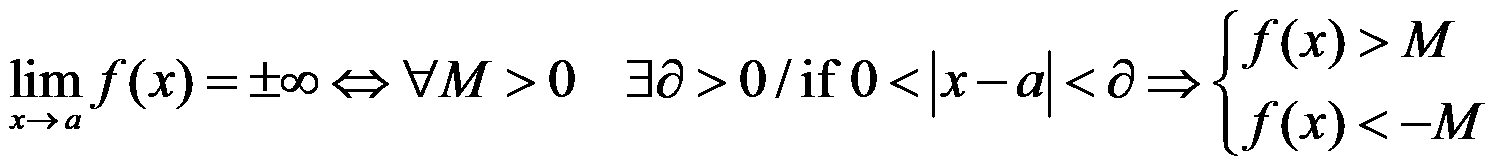
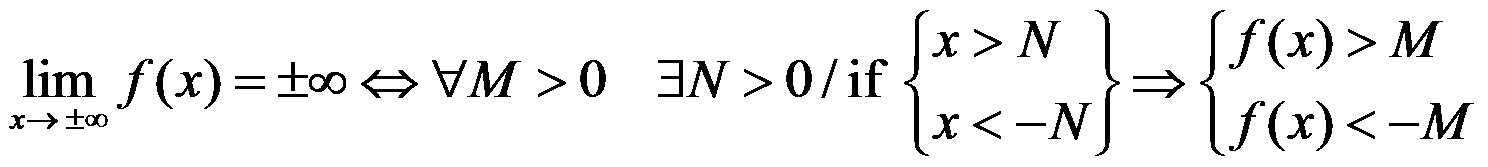
NOTE: Remember that when

we have a vertical asymptote

Properties:
 
5) If the limit exists, it is unique.

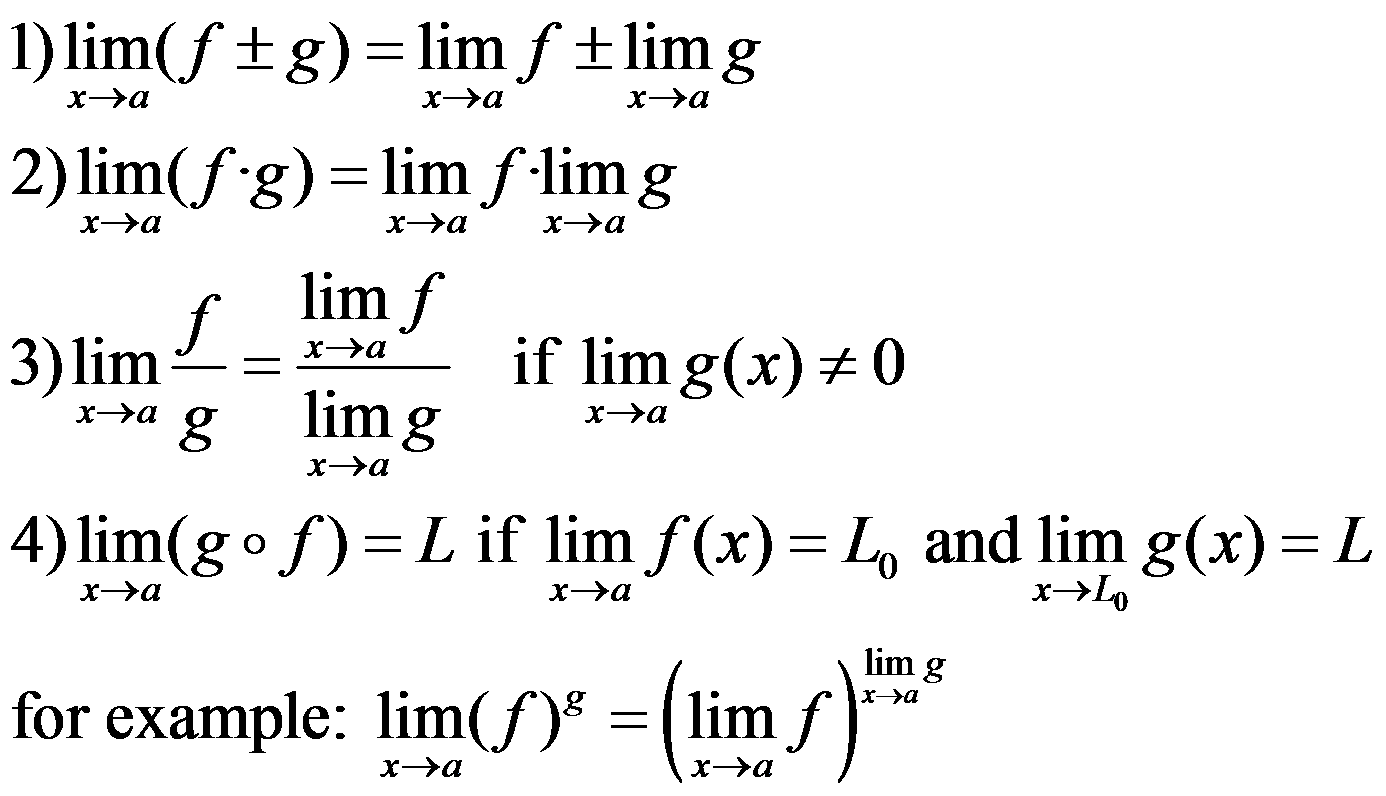
  Demonstration: Imagine we have two limits: b and c and b≠c. Then

 

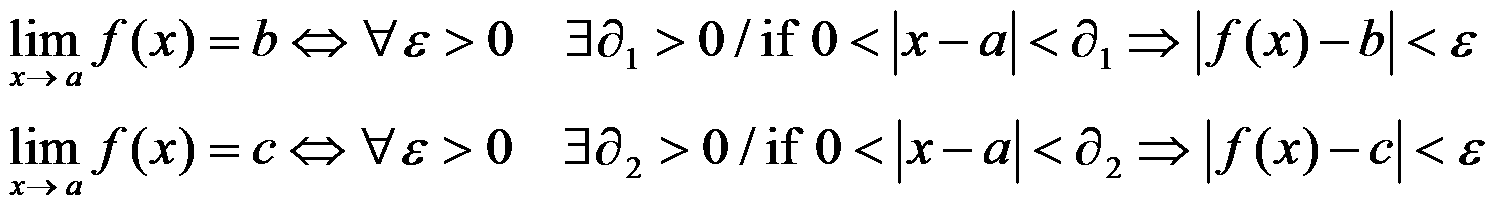
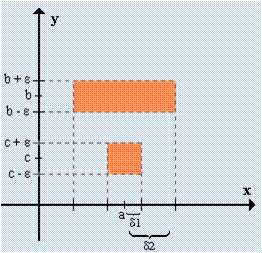
  If we choose ε as in the picture there is a contradiction in b using δ1. Then b = c and the limit is unique.

 

 Exercise: calculate the limit of f as x approaches 0 and 2, if:

 

 

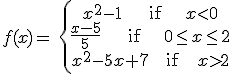
Solutions

 

 

 

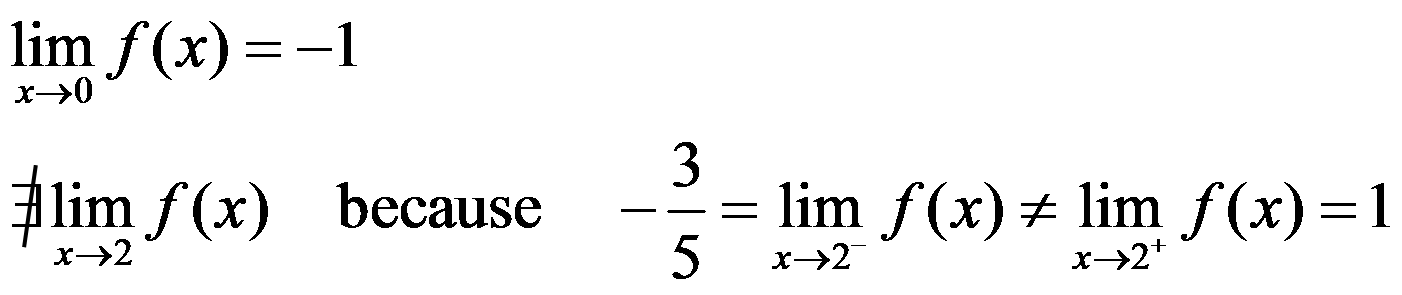
Licensed under the Creative Commons Attribution Non-commercial Share Alike 3.0 License