operations with functions
We define the addition, subtraction, multiplication and division of functions as:
· (f ± g)(x) = f(x) ± g(x)
· (f · g)(x) = f(x) · g(x)
· (f/g) (x) = f(x)/g(x) (if g(x)≠0)
Example: if f(x) = x2 -2 and g(x) = 3x + 2, then:
· (f + g)(x) = f(x) + g(x) = x2 + 3x
· (f - g)(x) = f(x) - g(x) = x2 – 3x - 4
· (f · g)(x) = f(x) · g(x) = 3x3 + 2x2 – 6x - 4
· (f/g) (x) = f(x)/g(x) = (x2 -2)/(3x + 2), if x ≠ -2/3
g°f(x) = g(f(x)) (if f(x)Є Dom g)
g°f(x) = g(f(x)) = g(x + 1) = (x + 1)2 = x2 + 2x +1
f°g(x) = f(g(x)) = f(x2) = x2 + 1
g°f ≠ f°g
f°f-1(x) = f(√x) = (√x)2= x
f-1 °f (x) = f-1(x2) = √x2 = x
f˚ f-1(x) = f(1/x) = 1/(1/x)= x
f-1 ˚f (x) = f-1(1/x) = 1/(1/x)= x
Example 3: find the inverse function of f(x) = √(2x)
x = √(2y) → x2 = 2y → y = f-1(x) = x2/2
NOTE: inverse functions are symmetric and their axis of symmetry is the line: y = x
Exercise:
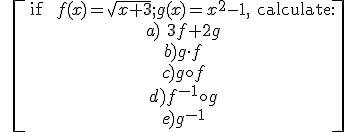
Solutions:

Licensed under the Creative Commons Attribution Non-commercial Share Alike 3.0 License