Limits of functions
Limits calculation
Examples:
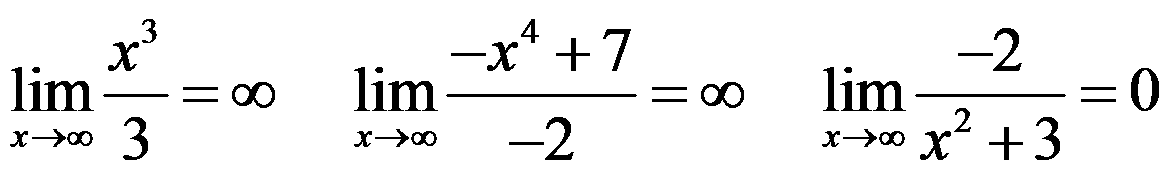
NOTE: remember that:
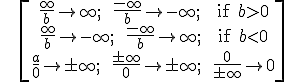
In infinite limits with polynomial functions, the limit is always ±∞ depending on the sign of the coefficient of the greatest degree term:
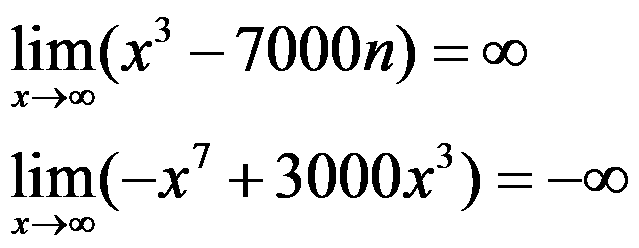
Undetermined forms of limits are the limits that are different depending on the situation. They are:
Infinite limits with rational functions always have an undetermined form of limit, which we have to solve by dividing by x to the highest power:
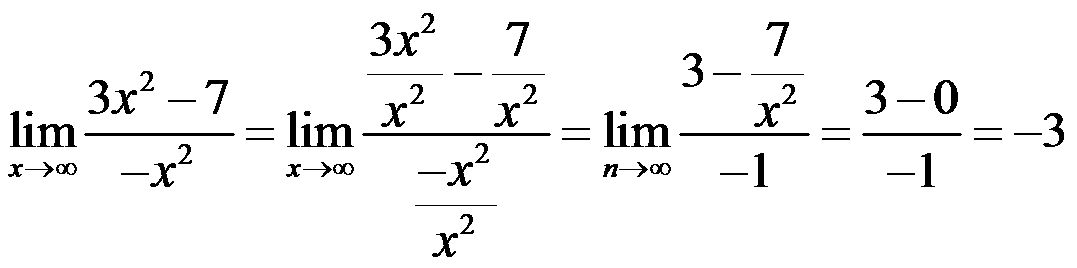
In the end:
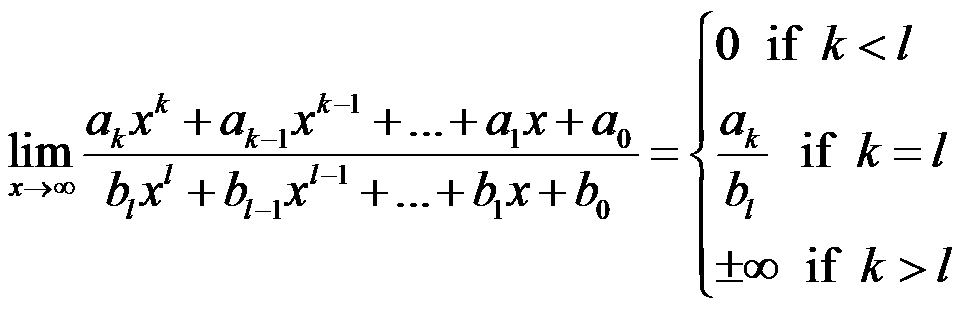
If we have irrational functions:
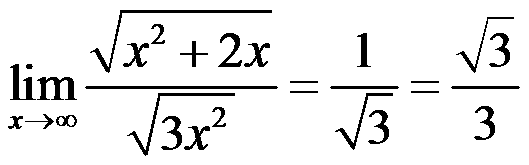
We can find an undetermined form of limit if we subtract square roots, then we have to use the conjugate to solve it:
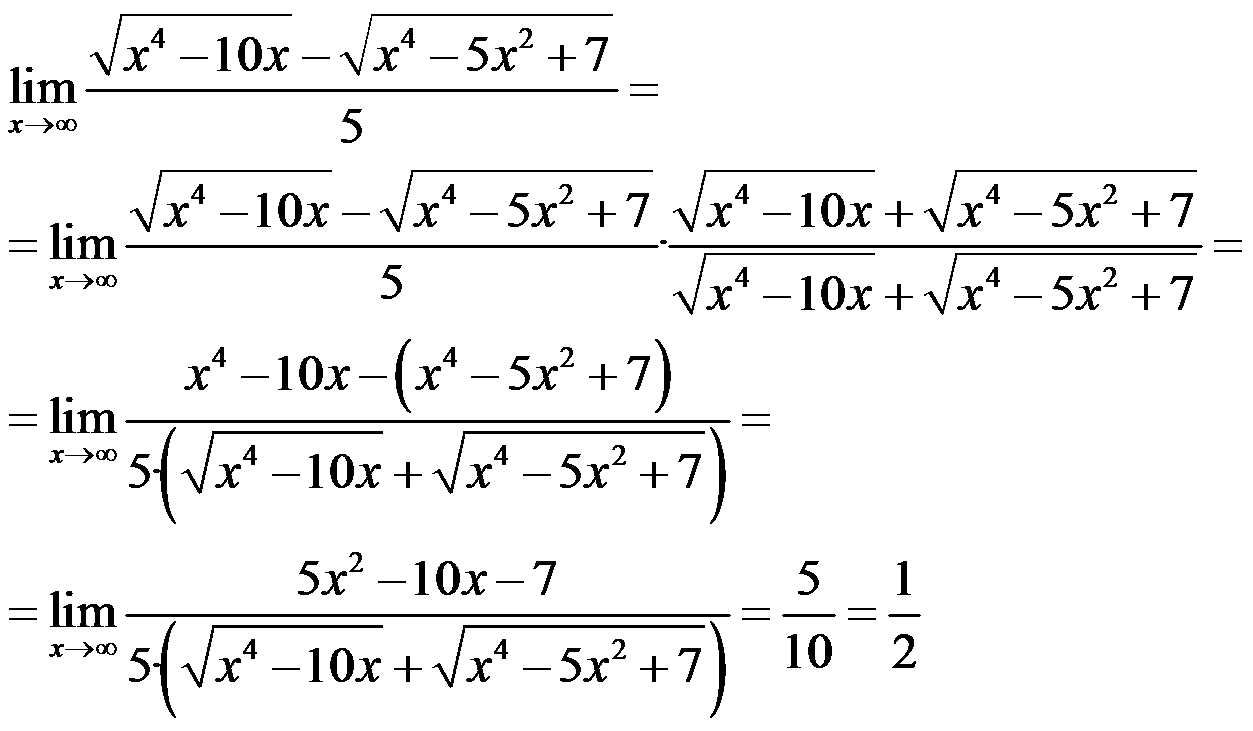
If a is -∞, then we change:
For example:
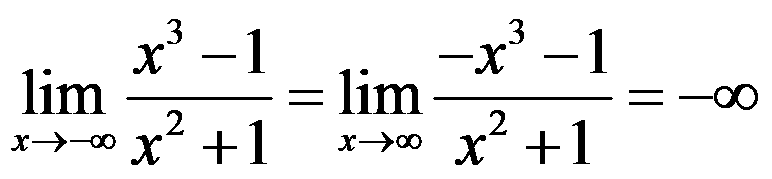
When a is not infinite, we can find other undetermined forms of limit:
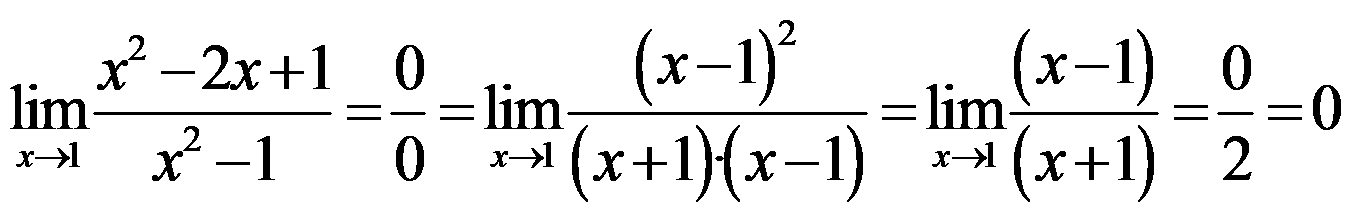
Other examples:
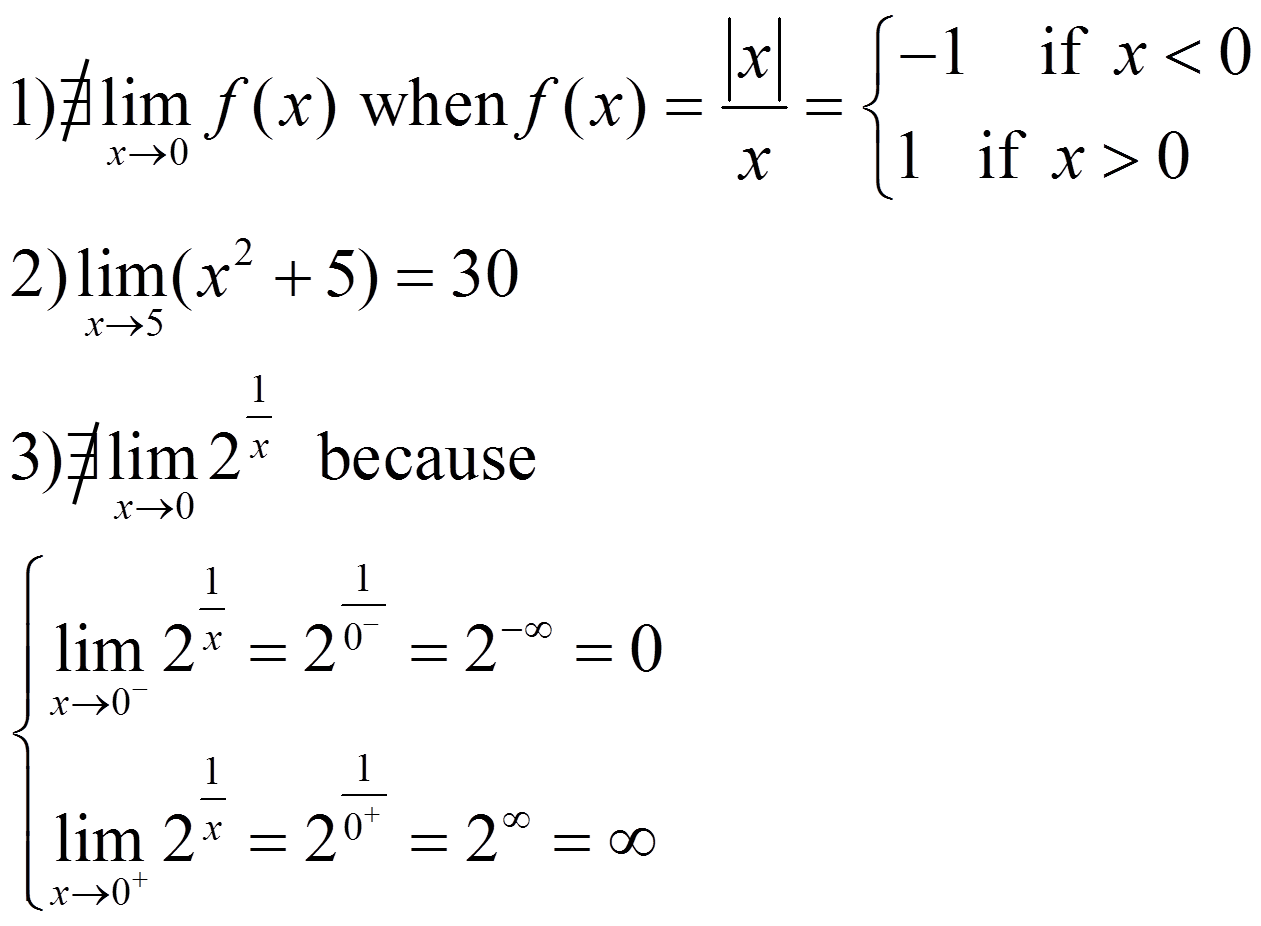
If the limit has powers, remember the property:
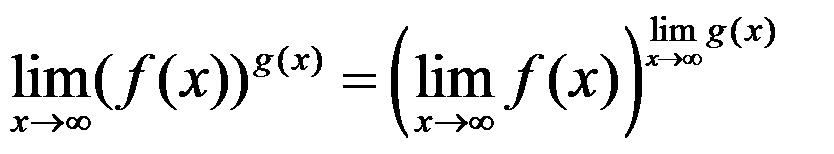
Examples:
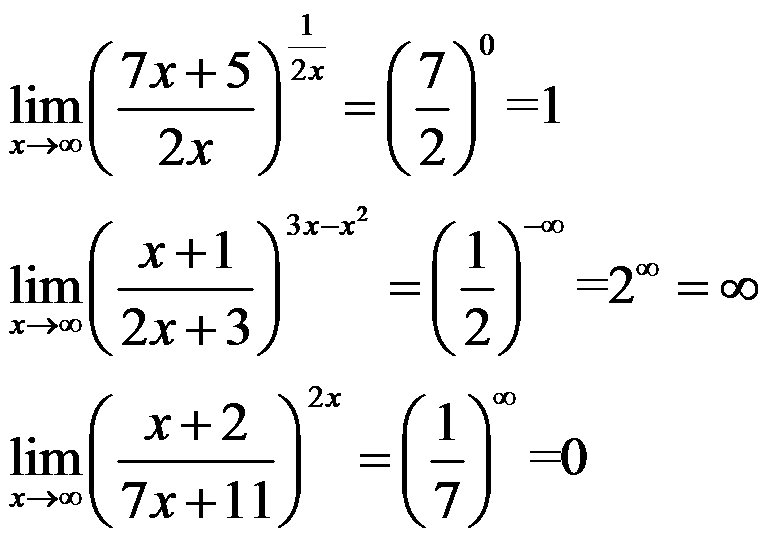
Number e is the limit:
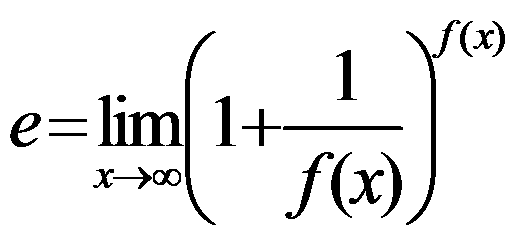
which is used in the undetermined form of limit 1∞
Example:
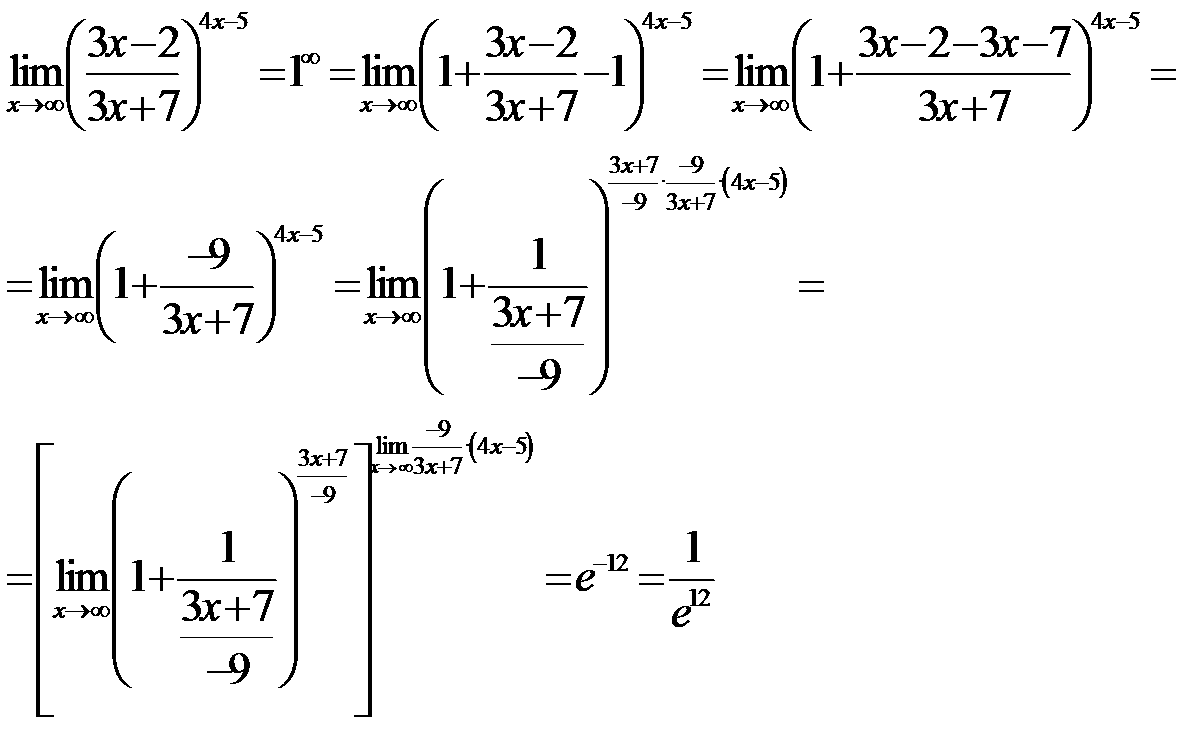
Exercise: calculate:

Solutions: a) 0; b) 1/2; c) 0; d) 1; e) -∞
Licensed under the Creative Commons Attribution Non-commercial Share Alike 3.0 License