Basis
k1u1 + k2u2 +….+ knun= 0 with some ki ≠ 0
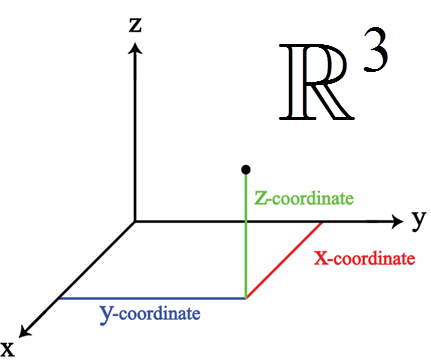
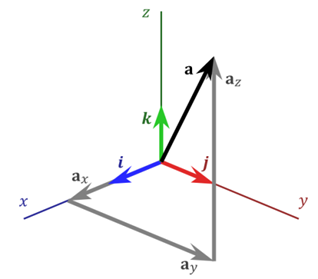
and there always exists an equipollent vector
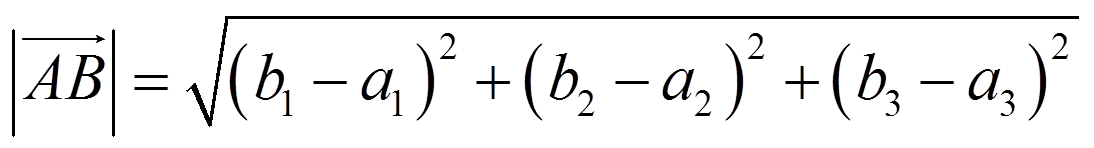
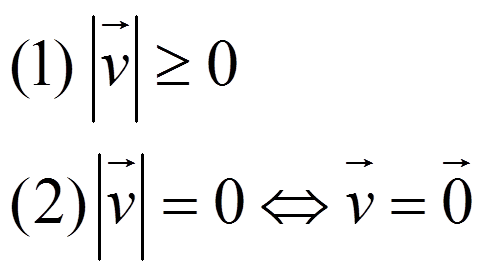
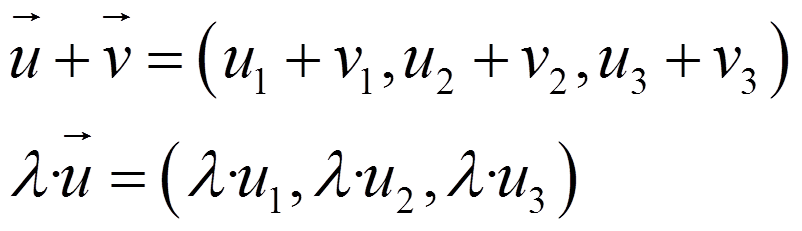
Exercises:
1.- If u(3,-2,1), v(1,3,-2), A(1,t,2), B(-3,3,0):
a) Calculate the magnitude of u.
b) Calculate t, if AB(-4,-2,-2).
c) Calculate u + v, 2u - 5v
2.- Decide if the following sets of vectors are linearly dependent, linearly independent, generative system and/or basis:
a) B1={(1,0,0),(1,1,0),(1,1,1)}
b) B2={(1,0,0),(0,1,0),(0,0,1),(1,1,1)}
c) B3={(1,1,1),(1,-1,3),(-1,3,-5)}
Solutions:
1.- a)|u|= √14; b) 5; c) u + v = (4,1,-1); 2u - 5v = (1,-19,12)
2.- a) Basis, generative system and linearly independent; b) linearly dependent and generative system; c) linearly dependent
Licensed under the Creative Commons Attribution Non-commercial Share Alike 3.0 License