Vector product

Let u and v linearly independent vectors. How do we determine all the vectors that are orthogonal to both of them?

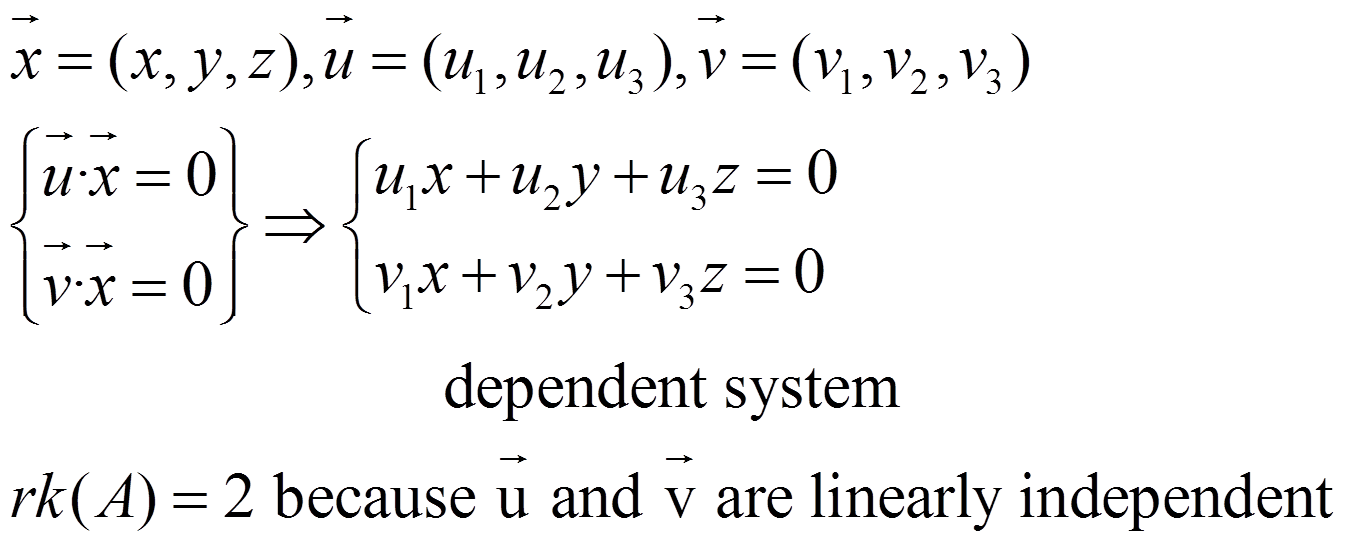
We can suppose that:

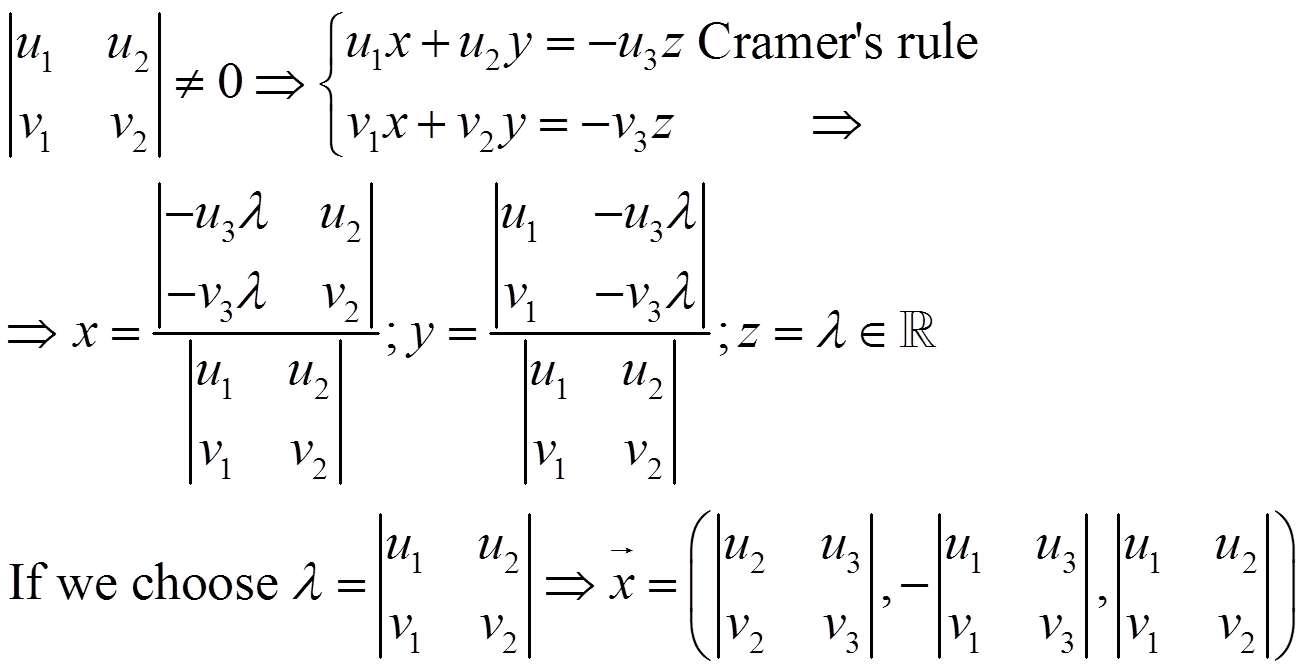
We name this vector

cross or vector product of u and v .

Then:

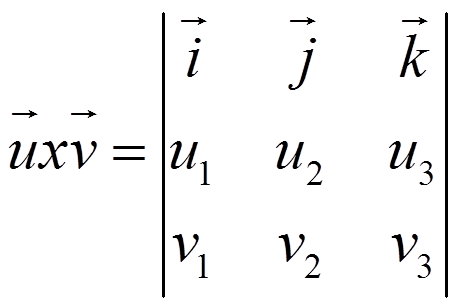
- Its magnitude is:

- Its direction is perpendicular to u and v.

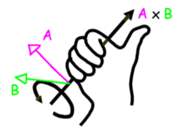
- Its sense is determined by the “corkscrew rule” or “right-hand rule”

Properties:

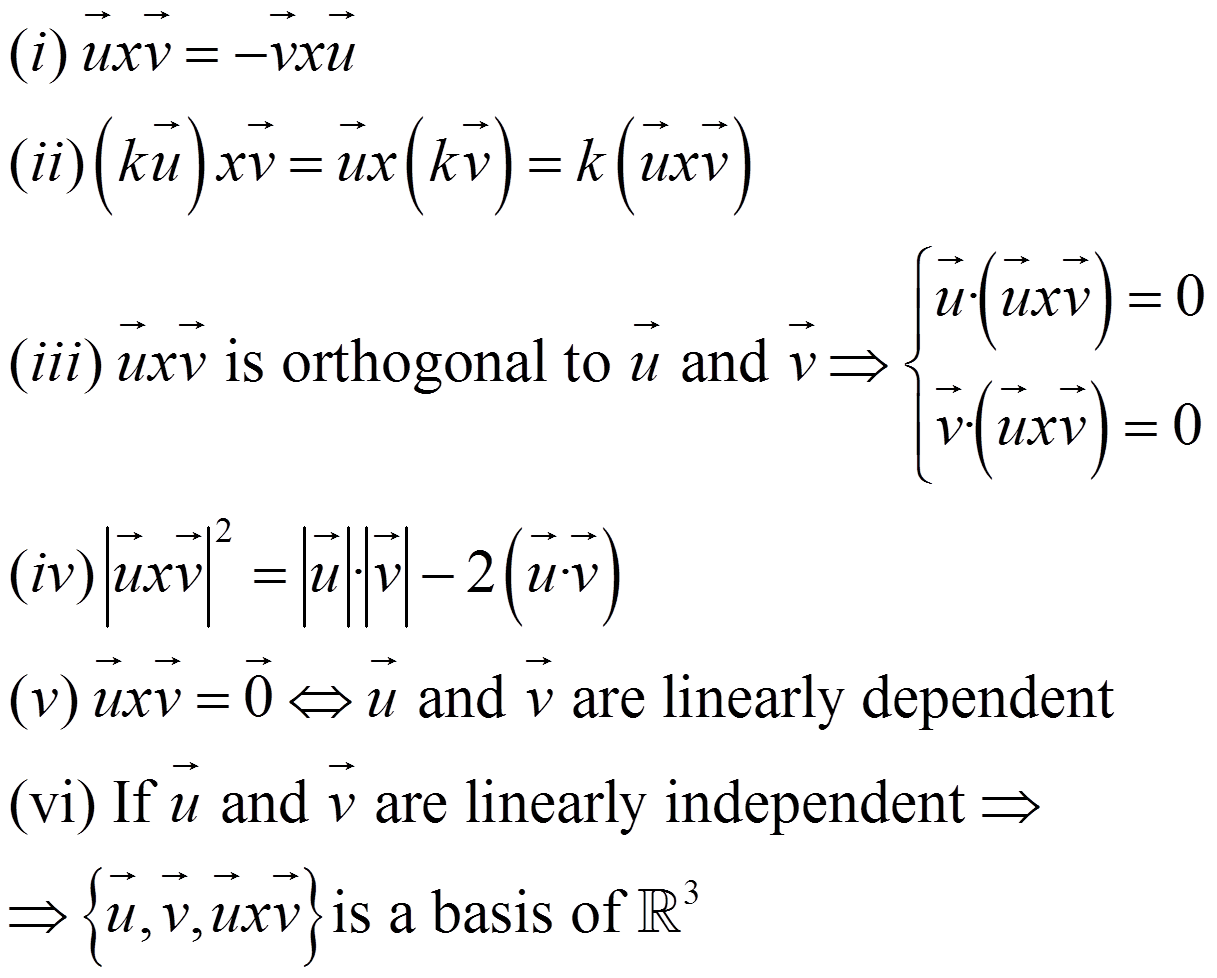
(vii) The area of the parallelogram formed by u and v is the magnitude of its vector product.

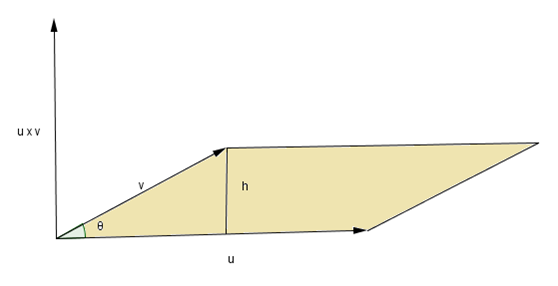
Demonstration:

Exercise: Let A(1,1,1),B(2,-1,0),C(3,3,-2). Calculate:

a) ABxAC

b) A unit vector orthogonal to AB and AC

c) The area of the parallelogram defined by the vectors AB and AC

d) The area of the triangle ABC

Solutions: a) (-4,1,-2); b) (-4√21/21,√21/21,-2√21/21); c) √21u²; d) √21/2u²