VectorsInSpace
operations with vectors
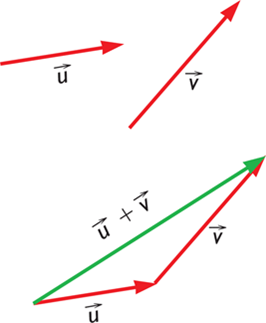
To add two vectors, u and v, we join the extreme of u with the origin of v and then, u + v has the origin of u as its origin and the extreme of v as its extreme.
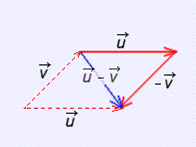
The opposite of a vector v, is another vector, -v, with the same magnitude and direction but opposite sense. The coordinates are the opposite of v-coordinates.
To subtract two vectors, u and v, we add u and –v.
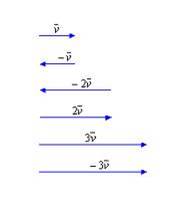
The multiplication of a vector v by a scalar λ (λЄR), is another vector, λv, with:
–magnitude:|λ|·|v|
–the same direction with the same sense if λ > 0, and opposite sense if λ < 0.
PROPERTIES: let u, v, w free vectors and λ, µ real numbers
(i) Commutative property: u + v = v + u
(ii) Associative property: u + (v + w) = (u + v) + w
(iii) Additive identity:
(iv) Additive inverse:
(v) Distributive properties:
(λ +µ)·u= λ·u + µ·u λ(u+v) = λ·u + λ·v
(vi)
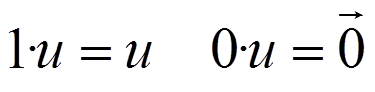
(vii) Triangle inequality: |u + v| ≤ |u| + |v|
With all these properties ,
Licensed under the Creative Commons Attribution Non-commercial Share Alike 3.0 License