VectorsInSpace
Scalar product
The scalar or dot product of two vectors, u and v, is the real number: u·v = u1·v1 + u2·v2 + u3v3
Properties:
- Commutative property: u·v = v·u
- Associative with respect to the multiplication by a scalar: (k·u)·v = k·(u·v) k€R
- Distributive property: u·(v + w) = u·v + u·w
- ![]()
- v·v = |v|2
- Cauchy-Schwartz inequality: |u·v| ≤ |u|·|v|
Theorem: if θ (≤ π) is the angle between u and v, then:
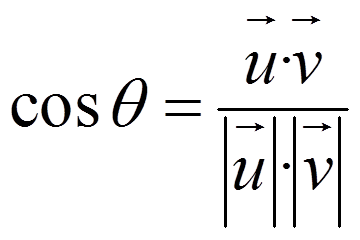
Demonstration:
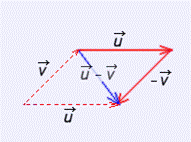
Cosine Theorem→ |u-v|2=|u|2+|v|2-2|u||v|cosθ
On the other hand: (u-v)2=(u-v)(u-v)=u2-uv-vu+v2=|u|2+|v|2-2uv
Joining: -2uv =-2|u||v|cosθ
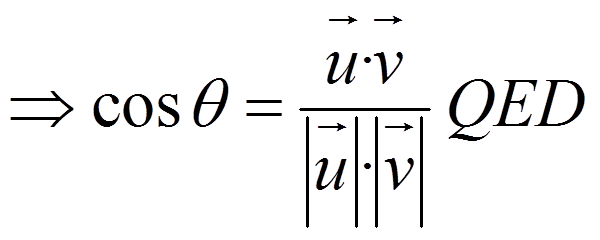
Then
![]()
Two vectors, u and v, are said to be orthogonal if u·v=0
Properties:
–If u = 0 → u is orthogonal to every vector
–If u,v ≠ 0, then: u·v = 0 ↔ θ = π/2
An orthonormal basis is formed by unit vectors that are orthogonal to each other.
For example, the canonical basis is an orthonormal basis.
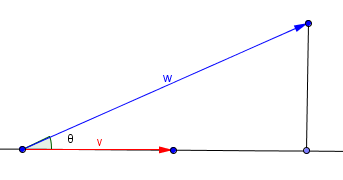
Let v and w two non-zero vectors. If w=w1+w2 with w1 parallel to v and w2 orthogonal to v, we say that w1 is the orthogonal projection of w over v and w2 its orthogonal component.
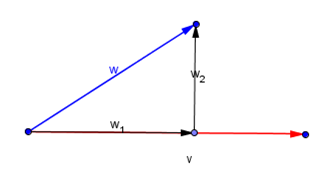
We name:
Then:
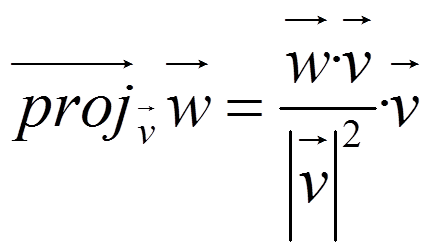
Demonstration:
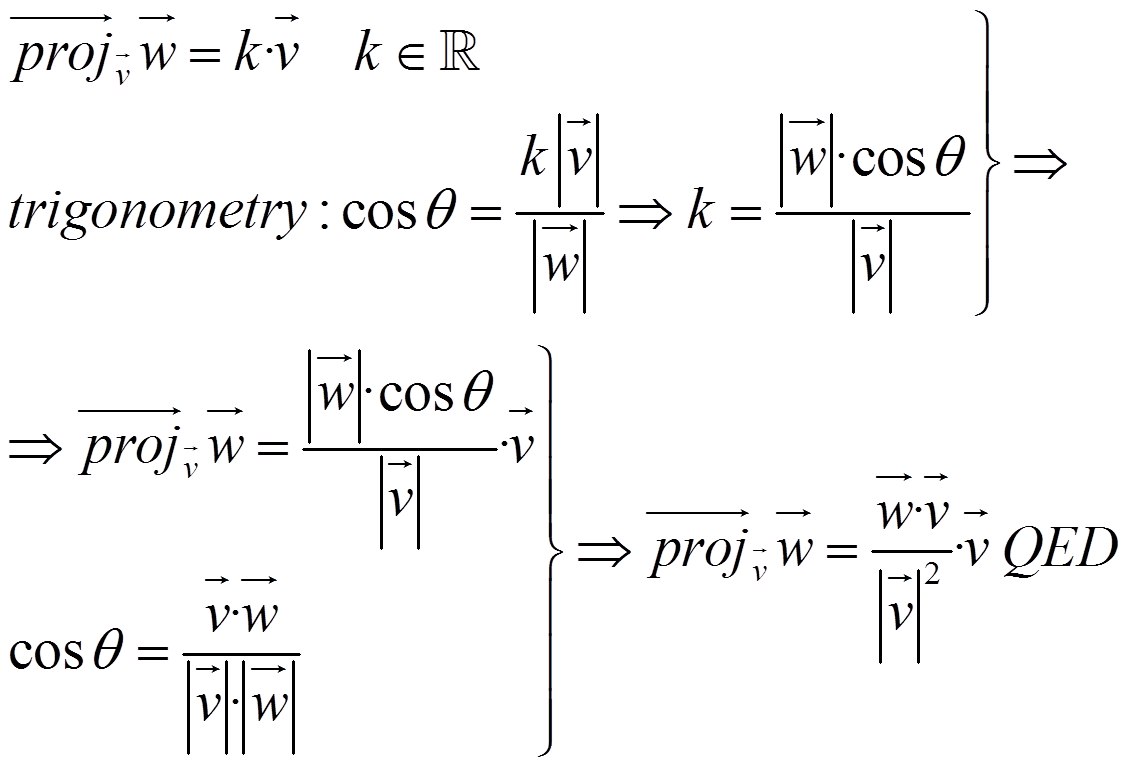
NOTE: If u is a unit vector
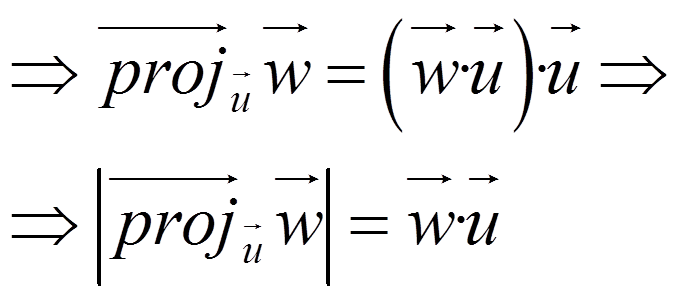
Then, the scalar product by a unit vector, u, measures the length of the orthogonal projection in the direction of u.
Exercises:
1.- Let u(-1,-1,2) and v(2,-3,1):
a) Calculate the angle that u and v form.
b) Calculate the orthogonal projection of u over v.
2.- Let the points A(1,-5,k), B(3,k,1), C(k,-5,2) the vertices of a triangle. Find the value of k that makes the triangle right-angled in A.
Solutions: 1.- a) 70o53'36''; b) (3/7,-9/14,3/4); 2.- k = 0 or k = 1
Licensed under the Creative Commons Attribution Non-commercial Share Alike 3.0 License