2. domain
If we talk about real functions with real variables:
- The domain of a polynomial function is always R.
Example: f(x) = 3x5 – 5x +243 Dom f = R
- We have to remove the roots of the denominator of a rational function from its domain.
Example:
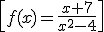
Dom f = R – {-2,2}
- The domain of an irrational function f(x) = √R(x) is Dom f = {x,R(x)≥ 0}
Example: f(x) = √(x2 – 3x + 2)
Dom f = (-∞,1]U[2,∞)
- The domain of a logarithmic function f(x) = loga L(x) is Dom f = {x,L(x)> 0}
Example: f(x) = ln(7x – 21)
Dom f = (3,∞)
Exercise: find the domain of these functions:
a) f(x) = 3x5- 5x2 - 7x +3
b) ![]()
c) ![]()
d) f(x) = log2 (x2 - 4x + 4)
Solutions: a) R; b) R - {0, 2, 4}; c) (-∞,-2]U[2,∞); d) R - {2}
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 3.0